- #1
D44
- 70
- 0
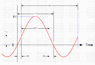
I have to calculate the RMS and average voltage of a sine wave with a DC offset.
I have a peak to peak voltage of 11V and an offset which is -6V.
I have the average voltage as -6V and RMS voltage as 7.15V. I calculated the RMS as follows:
AC Vrms = 5.5/sqrt(2) = 3.89V
Vrms = sqrt(3.89^2 + 6^2) = 7.15V
Does this look correct?
I have a peak to peak voltage of 11V and an offset which is -6V.
I have the average voltage as -6V and RMS voltage as 7.15V. I calculated the RMS as follows:
AC Vrms = 5.5/sqrt(2) = 3.89V
Vrms = sqrt(3.89^2 + 6^2) = 7.15V
Does this look correct?