- #1
togo
- 106
- 0
Homework Statement
The area bounded by the x-axis and curve
y = 4-x^2
is rotated about x-axis, find the volume.
Homework Equations
[integral] pi y^2 dx
The Attempt at a Solution
the answer is supposed to be 512/15 pi
Your answer is equivalent to (256/15)π .togo said:Homework Statement
The area bounded by the x-axis and curve
y = 4-x^2
is rotated about x-axis, find the volume.
Homework Equations
[integral] pi y^2 dx
The Attempt at a Solution
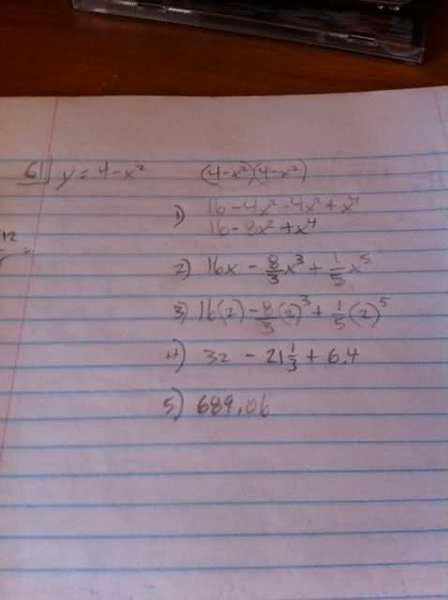
the answer is supposed to be 512/15 pi
If you integrate this function, which is even, from -2 to 2, you should get twice the result that you get by integrating from 0 to 2.togo said:Understood. I did integrate with 2 only. So I should be integrating from -2 to 2. I quickly did that calculation and came up with -48.93333 using the -2. That can't be right.
so you're saying that -2 and 2 shouldn't be used since the y-axis is not a boundary?
EDIT: I got it, integrating -2 answer -17.067
The formula for finding the volume of an area revolved around the x axis is V = π∫(f(x))^2 dx, where f(x) represents the function defining the area and the integral is taken with respect to x.
The difference between finding the volume of a solid and finding the volume of an area revolved around the x axis lies in the shape of the object. While finding the volume of a solid involves calculating the amount of space inside a 3-dimensional object, finding the volume of an area revolved around the x axis involves calculating the amount of space inside the 3-dimensional shape created by revolving a 2-dimensional area around the x axis.
Yes, the formula V = π∫(f(x))^2 dx can be used for any shape as long as the function f(x) defining the area is known. This formula is especially useful for finding the volume of complex 3-dimensional shapes that cannot be easily calculated using traditional methods.
The units for the volume of an area revolved around the x axis will depend on the units of the function f(x). For example, if f(x) is given in meters, the volume will be in cubic meters (m^3). It is important to make sure all units are consistent when using this formula.
Yes, there are certain situations where the formula V = π∫(f(x))^2 dx cannot be used. This formula assumes that the 2-dimensional area being revolved is continuous and has a single defining function f(x). If the area is discontinuous or has multiple defining functions, a different method must be used to find the volume.