Two Masses, a Pulley, and an Inclined Plane

[ElectricMile]

so frikin confused tried too many times, can anyone help me out?

*image attached*

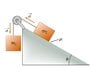
Block 1, of mass m_1, is connected over an ideal (massless and frictionless) pulley to block 2, of mass m_2, as shown. Assume that the blocks accelerate as shown with an acceleration of magnitude a and that the coefficient of kinetic friction between block 2 and the plane is mu.

Find the ratio of the masses m_1/m_2.
Express your answer in terms of some or all of the variables a, mu, and theta, as well as the magnitude of the acceleration due to gravity g.

 

[p53ud0 dr34m5]

first, try drawing a free body diagram. this will let you know what all forces are acting on the two objects. then, think of how you can relate the normal force to friction and the coefficient of friction.

 

[Norman]

In general when working out problems of this type it is useful to have a plan of attack. And for problems of this type there is definitely a common set of steps that will help you get started.
Steps for solving Force Problems:
1) Make a Drawing
2) Draw your free-body diagrams making sure to include ALL the forces acting on that body.
3) choose a "useful" coordinate system.
4) Write Newton's Second Law for all the bodies involved in they system.
5) Do the Math.

A couple of notes:
When you are drawing your free-body diagrams remember it is only the forces acting on that body.
When you are choosing your coordinate system (in physics you are free to choose any coordinate system you like- the trick is using one that makes your life easy) typically you will try to choose a coordinate system in which the acceleration is only in one of the dimensions.

 

[ElectricMile]

still don't get it drawn the free body diagrams and not understanding how to construct the formula, can anyone help?

 

[marlon]

On the mass m2 you will have the following forces

1) friction force $$\mu N$$
2) Normal force N
3) gravity
4) force from mass m1 equal to m1 * g

Suppose the x-axis is along the incline pointing upward toward the pulley...

$$m_2 a_x =- \mu N -m_2 gsin(\theta) +m_1g$$
$$m_2 a_y = N -m_2 gcos(\theta)$$

the clue is that the gravity on m_2 needs to be projected onto the x and y axis, hence the sine and cosine.

This should get you started...this is the most difficult part

marlon

 

[ElectricMile]

so wait would

(m_1)ax= (m_1)*g
and
(m_1)ay=o

?
or am i just really confused,

if so then how do i intergrate m_2ay & m_2ax into an m_2a equation?

 

[marlon]

so wait would

(m_1)ax= (m_1)*g
and
(m_1)ay=o

?
or am i just really confused,

if so then how do i intergrate m_2ay & m_2ax into an m_2a equation?

Where did you get this ?
This is wrong : The x-axis is ALONG the incline

You need to realize that of the x-axis is along the incline, the y-axis is perpendicular to the incline. Since you keep on moving on the incline, you must have NO NOT force along the y-axis so m_2*a_y = 0. Knowing this, you can solve the second equation in my first post in order to get to N. Then plug this N into the first equation.

The trick is to look only at the second mass on the incline. m_1 is automatically incorporated because of the force in the rope between the two masses. I gave you all you need, you only need to calculate right now.

marlon

 

[ElectricMile]

ok this just really confused me, N is equal to normal force right? and this just boggled me even more

im not solveing for any numbers I am trying to find the equation using the variables which is even more confusing.

 

[marlon]

ok this just really confused me, N is equal to normal force right? and this just boggled me even more

im not solveing for any numbers I am trying to find the equation using the variables which is even more confusing.

The Normal force is directed perpendicular to the incline (along the y-axis).

read my first post and tell me how the 4 forces on m_2 are directed along the x and y-axis. This should clarify alot...

marlon

 

[ElectricMile]

for m_2

friction and tension are on x
N normal is on y
and m_2*g is between neg y and x axis

 

[marlon]

for m_2

friction and tension are on x
N normal is on y
and m_2*g is between neg y and x axis

That is correct. Now, the trick is the project the gravity on m_2 onto the x and y-axis. You will need trigoniometry for that. I wrote the formula's with the sine and cosine... Make sure you can get to these formula's yourself

marlon

 

[ElectricMile]

alright but won't i need to have these two formulas into one, and put this over the m_1 formula?

 

[Doc Al]

On the mass m2 you will have the following forces

1) friction force $$\mu N$$
2) Normal force N
3) gravity

Right.

4) force from mass m1 equal to m1 * g

Incorrect. The tension pulls on m2, but is not equal to m1*g.

The way to solve this problem is to apply Newton's 2nd law separately to m1 and m2. Consider force components in the direction of motion.

For m1: The forces are:

$m_1 g$ (down)
tension (T) (up)​

The acceleration is "a" (down): Apply Newton's 2nd law.

For m2: The forces (parallel to the incline) are:

$m_2 g sin\theta$(down the incline)
tension (T) (up the incline)
friction ($\mu N$) (down the incline)​

The acceleration is "a" (up the incline): Apply Newton's 2nd law. (Use marlon's advice to find the normal force.)

You'll have two equations. Eliminate T and you'll be able to find the ratio of the masses.

 

[Kevin713]

Sorry to resurrect this old topic. I've had a problem exactly like this a couple nights ago, and I spent hours trying to examine all of the angles. In this case, we're assuming that Block 1 is accelerating downwards, thereby pulling Block 2 up the incline. If this is true, then the solution is as well.

I previously thought that even if this wasn't true, if our acceleration value comes up negative, we can simply reverse our assumed direction, and just keep the same magnitude.

But after solving many problems like this, I now think differently (maybe I'm wrong). If the acceleration is indeed in the direction of Block 1, then these steps (listed by Doc Al) are definitely correct:

...
For m1: The forces are:

LaTeX Code: m_1 g (down)
tension (T) (up)

The acceleration is "a" (down): Apply Newton's 2nd law.

For m2: The forces (parallel to the incline) are:

LaTeX Code: m_2 g sin\\theta (down the incline)
tension (T) (up the incline)
friction (LaTeX Code: \\mu N ) (down the incline)

The acceleration is "a" (up the incline): Apply Newton's 2nd law
...

But, if the acceleration is in the direction of Block 2 (pushing it down the incline, and pulling Block 1 up), then for m2 shouldn't it be:

m2gsin(theta) (down incline)
Tension T (up incline)
Friction mu*N (up incline)

?

Maybe this is too obvious, but I ask because if true (acceleration down the incline), once you solve for it this way, the magnitude of acceleration will not be the same as with the previous assumption (acceleration up the incline).

Obviously, this can be cleared up if you just do some simple calculations at first, and calculate which direction the net force/acceleration is in. But I've encountered many postings online of people claiming that it doesn't matter what direction you assume a to be - the calculations will not change the magnitude, simply the sign.

Which is true?

Any responses would be appreciated, as I'm under some time pressure...