- #1
inferno298
- 25
- 0
Homework Statement
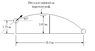
A regulation volleyball court is L = 18.0 m long and a regulation volleyball net is d = 2.43 m high. A volleyball player strikes the ball a height h = 1.73 m directly above the back line, and the ball's initial velocity makes an angle theta = 40 degrees with respect to the ground.
1)In volleyball, it is often advantageous to serve the ball as hard as possible. If you want the ball to land in the opponent's court, however, there is an upper limit on the initial ball speed for a given contact point. At this maximum speed, the ball just barely makes it over the net and then just barely lands in bounds on the back line of the opponent's court. For the contact point given in the previous problems, what is this maximum initial speed?
2)If you hit the ball at this maximum speed, at what angle should you strike it in order to make sure the ball lands in bounds?
Homework Equations
Projectile motion equations
Y = Yo + Vyo*t- 0.5*g*t^2
X = Vx*t
And the derivative of those equations.
The Attempt at a Solution
I sure I can solve number 2 fine, I just need helping starting number 1. Kind of lost on where to begin and what to start with. Any help would be very much appreciated!