- #1
AntiElephant
- 25
- 0
I'm trying to understand the form of the absorption spectrum of a T=0K intrinsic semiconductor. The valence band/conduction band energy diagram looks like;
http://postimg.org/image/wyzvo9lsr/
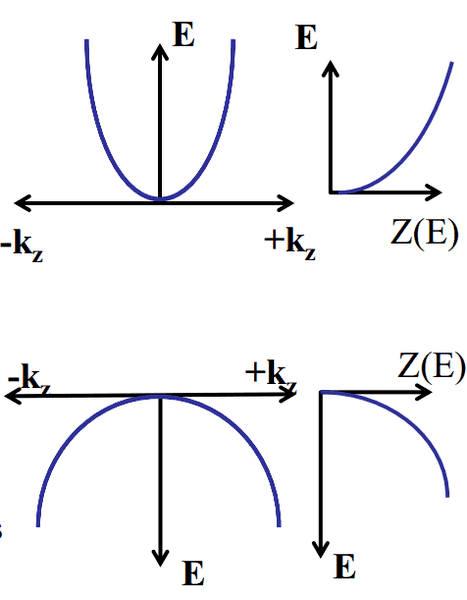
As [itex] E = \frac{\hbar^2 k^2}{2m^*} [/itex]
where [itex] m^* [/itex] denotes the effective mass. The image doesn't indicate too well that the effective mass in the valence band is MUCH larger than that in the conduction band.
I'm trying to understand the absorption spectrum of photons sent into the semiconductor. For photons with energy less than the band gap there is no absorption.
When photons with energy more than the band gap are sent in, there is absorption. We assume that the momentum of the photons is low and so in the diagram above there can only be vertical transitions from the valence to the conduction band - so the transition energies are uniquely determined (i.e. an electron is promoted from [itex] E_2 [/itex] to [itex] E_1 [/itex] and [itex] E_1,E_2[/itex] are uniquely determined).
I would hazard a guess that the absorption spectrum is proportional to the product of the density of states [itex] Z(E_1)Z(E_2) [/itex]. There are two ways I can interpret this...
1) Examine the change of the absorption spectrum from a photon energy [itex] E [/itex] to a small increase [itex] E + \Delta E [/itex]. For a vertical transition, [itex] E_2 [/itex] barely changes because the effective mass in the valence band is so large, but [itex] E_1 [/itex] changes quite rapidly since it is so low in the conduction band. So [itex] Z(E_2) [/itex] is practically constant and so the absorption spectra depends only on [itex] Z(E_1) [/itex]. Since [itex] Z(E_1) \propto E_1^{1/2} [/itex] we see the absortion spectrum increase like [itex] E^{1/2} [/itex].
2) Mathematically you can see, since the momentum is conserved
[itex] E_1 = \frac{\hbar^2 k^2}{2m_c^*} [/itex]
[itex] E_2 = \frac{\hbar^2 k^2}{2m_v^*} [/itex]
[itex] E_1/E_2 = m_v^*/m_c^* [/itex]
Then the absorption rate is [itex] \propto Z(E_1)Z(E_2) \propto (E_1 E_2)^{1/2} \propto E_1 [/itex]
And so it varies linearly with [itex] E_1 [/itex] and hence the energy of the photon.
I'm told actually it varies like [itex] E^{1/2} [/itex] which would imply the second way is wrong. But how does the maths lie?
{Edit: I've included the image so that one doesn't have to click the link to see it - Zz}
http://postimg.org/image/wyzvo9lsr/
As [itex] E = \frac{\hbar^2 k^2}{2m^*} [/itex]
where [itex] m^* [/itex] denotes the effective mass. The image doesn't indicate too well that the effective mass in the valence band is MUCH larger than that in the conduction band.
I'm trying to understand the absorption spectrum of photons sent into the semiconductor. For photons with energy less than the band gap there is no absorption.
When photons with energy more than the band gap are sent in, there is absorption. We assume that the momentum of the photons is low and so in the diagram above there can only be vertical transitions from the valence to the conduction band - so the transition energies are uniquely determined (i.e. an electron is promoted from [itex] E_2 [/itex] to [itex] E_1 [/itex] and [itex] E_1,E_2[/itex] are uniquely determined).
I would hazard a guess that the absorption spectrum is proportional to the product of the density of states [itex] Z(E_1)Z(E_2) [/itex]. There are two ways I can interpret this...
1) Examine the change of the absorption spectrum from a photon energy [itex] E [/itex] to a small increase [itex] E + \Delta E [/itex]. For a vertical transition, [itex] E_2 [/itex] barely changes because the effective mass in the valence band is so large, but [itex] E_1 [/itex] changes quite rapidly since it is so low in the conduction band. So [itex] Z(E_2) [/itex] is practically constant and so the absorption spectra depends only on [itex] Z(E_1) [/itex]. Since [itex] Z(E_1) \propto E_1^{1/2} [/itex] we see the absortion spectrum increase like [itex] E^{1/2} [/itex].
2) Mathematically you can see, since the momentum is conserved
[itex] E_1 = \frac{\hbar^2 k^2}{2m_c^*} [/itex]
[itex] E_2 = \frac{\hbar^2 k^2}{2m_v^*} [/itex]
[itex] E_1/E_2 = m_v^*/m_c^* [/itex]
Then the absorption rate is [itex] \propto Z(E_1)Z(E_2) \propto (E_1 E_2)^{1/2} \propto E_1 [/itex]
And so it varies linearly with [itex] E_1 [/itex] and hence the energy of the photon.
I'm told actually it varies like [itex] E^{1/2} [/itex] which would imply the second way is wrong. But how does the maths lie?
{Edit: I've included the image so that one doesn't have to click the link to see it - Zz}
Last edited by a moderator: