- #1
euclideanspace
- 22
- 0
L=0 Suborbital Configuration
These questions are directed at resident theoretical quantum physicists in PF
Regarding suborbitals L 0 I → L 0 VII corresponding to Periods 1 - 7
A total of 14 electron positions exist within Azimuthal Quantum Energy State 0 in Periods 1 through 7
Additionally, Azimuthal Quantum State 0 represents a 0° orbital plane angle along an x-y axis,
and a limit of 1 electron pair perL 0 suborbital;
This suggests 7 discrete coaxial suborbital shells for L 0 without violating the Pauli exclusion principle.
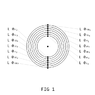
Figure 1 illustrates 7 coaxial L 0 suborbital shells and 14 electron positions,
numbered L 0 I → L 0 VII, with 7 electron pairs aligned along the y axis, each electron representing 1 standing wave nodal loop,
and the crest of each node being 1 negative point charge.
Question 1 : Are the 7 suborbital shells illustrated in Figure 1 in agreement with the current standard model?
Regarding Azimuthal Quantum Energy States : L+1ħ, +2ħ, +3ħ → ]L -1ħ, -2ħ, -3ħ
with the point charges at each node counted as discrete electrons
which would result in :
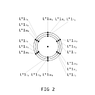
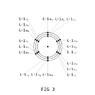
3 suborbital shells (x 2) for L +1ħ and -1ħ respectively, with 6 electrons (nodal point charges) per suborbital shell per suborbital shell
a total of 36 electron positions for Periods 2 → 7
L +1ħ and -1ħ illustrated in Figure 2 and Figure 3
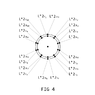
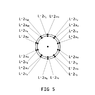
2 suborbital shells (x 2) for L +2ħ and -2ħ respectively, with 10 electrons (nodal point charges) per suborbital shell,
a total of 40 electron positions for Periods 4 → 7
L +2ħ and -2ħ illustrated in Figure 4 and Figure 5
and
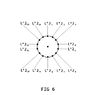
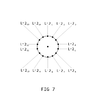
1 orbital shell (x 2) for L +3ħ and -3ħ respectively, with 14 electrons (nodal point charges) per orbital shell
a total of 28 electron positions for Periods 6 → 7
L +3ħ and -3ħ illustrated in Figure 6 and Figure 7
Question 2 : Are the suborbital shells illustrated in Figures 2 → 7 in agreement with the current standard model?
Thanks in advance
~ E:S
These questions are directed at resident theoretical quantum physicists in PF
Regarding suborbitals L 0 I → L 0 VII corresponding to Periods 1 - 7
A total of 14 electron positions exist within Azimuthal Quantum Energy State 0 in Periods 1 through 7
Additionally, Azimuthal Quantum State 0 represents a 0° orbital plane angle along an x-y axis,
and a limit of 1 electron pair perL 0 suborbital;
This suggests 7 discrete coaxial suborbital shells for L 0 without violating the Pauli exclusion principle.
Figure 1 illustrates 7 coaxial L 0 suborbital shells and 14 electron positions,
numbered L 0 I → L 0 VII, with 7 electron pairs aligned along the y axis, each electron representing 1 standing wave nodal loop,
and the crest of each node being 1 negative point charge.
Question 1 : Are the 7 suborbital shells illustrated in Figure 1 in agreement with the current standard model?
Regarding Azimuthal Quantum Energy States : L+1ħ, +2ħ, +3ħ → ]L -1ħ, -2ħ, -3ħ
with the point charges at each node counted as discrete electrons
which would result in :
3 suborbital shells (x 2) for L +1ħ and -1ħ respectively, with 6 electrons (nodal point charges) per suborbital shell per suborbital shell
a total of 36 electron positions for Periods 2 → 7
L +1ħ and -1ħ illustrated in Figure 2 and Figure 3
2 suborbital shells (x 2) for L +2ħ and -2ħ respectively, with 10 electrons (nodal point charges) per suborbital shell,
a total of 40 electron positions for Periods 4 → 7
L +2ħ and -2ħ illustrated in Figure 4 and Figure 5
and
1 orbital shell (x 2) for L +3ħ and -3ħ respectively, with 14 electrons (nodal point charges) per orbital shell
a total of 28 electron positions for Periods 6 → 7
L +3ħ and -3ħ illustrated in Figure 6 and Figure 7
Question 2 : Are the suborbital shells illustrated in Figures 2 → 7 in agreement with the current standard model?
Thanks in advance
~ E:S