Inflationary Misconceptions and the Basics of Cosmological Horizons
Table of Contents
Introduction
It is a common saying that during inflation “space expanded faster than the speed of light.” This statement is meant to articulate the extreme rates of expansion seen during inflation, and this it does successfully. Unfortunately, it is at least a little wrong, and what little there is right about it is not unique to inflation. In this note, I hope to correct this misconception and explain what is so special about inflationary expansion. I suspect that this misconception persists because the relevant parts of the science are a little complicated, and don’t find their way into popular accounts. Readers familiar with the paper by Davis and Lineweaver [1] will find some overlap here, but my goal is to present the key ideas at a popular level, without assuming any prior understanding of cosmology. You will, however, need to know a smidge of calculus.
To set the groundwork: inflation is the name for a brief flash of accelerated expansion that took place when the universe was very young. Besides this period of primordial inflation and the dark energy-fueled acceleration of recent years, the universe spent a majority of its time — its formative years — decelerating. Accelerated expansion is indeed unusual, and it makes for a very interesting cosmological history.
The Universe as a balloon
In an effort to dispel inflationary misconceptions, it is necessary to correct a few misunderstandings related to expansion more generally. Expansion is so central to our understanding of the universe that we can’t skimp on this — erroneous misapprehensions simply will not do! The best way to model the expanding universe is with a balloon. Like an actual, three-dimensional balloon. Draw several dots on the balloon with a marker, and blow it up. The dots are galaxies, and the rubber surface of the balloon is space. Yes, this is a lower-dimensional analog: our three-dimensional universe has been flattened to the two-dimensional surface of the balloon. Decline urges to wonder about the inside of the balloon — it is not part of the analogy and the only thing that can be found there are socks that go missing from the dryer1. People think this makes the balloon model a bad analogy, and it’s true that it has its limits. But I contend that it does a great job of modeling how expansion actually happens: as you inflate the balloon, the points separate on account of the expanding rubber2. At no time are the points themselves moving relative to the rubber surface — they are fixed to it, moving along with the expansion. What the model demonstrates so clearly is that there is no center of the universe, no center to the expansion. From each dot’s perspective, all the other dots are moving away from it — each dot of course feels like it occupies a privileged spot at the center of the universe, but this is an illusion born out of the spherical symmetry and uniformity of the expansion.
Fig. 1. Balloon analogy. Girl not part of the analogy (no force is needed to expand the universe).
The balloon analogy also nicely demonstrates Hubble’s Law: [itex]v_{\rm rec}=Hr[/itex], that for a given rate of expansion, [itex]H[/itex], the greater the distance between two objects, [itex]r[/itex], the faster they recede from one another, [itex]v_{\rm rec}[/itex]. How does this work? Consider two points separated by some distance, and imagine dividing the intervening rubber of the balloon’s surface into many tiny increments. The further apart the two points, the more rubber there is between them, and so the more increments. Each increment will expand by the same amount in a given time, leading to a larger total expansion per unit time than that between more closely separated points. This is why it is not correct to refer to the speed of the expansion — the expansion proceeds at a fixed rate, [itex]H[/itex], but the speeds at which the dots recede from each other vary according to their separations! This is the first misconception embedded in the broader misconception that space expands faster than light during inflation. Space does not expand at a given speed, it is actually a speed per distance of separation (the units of [itex]H[/itex] are typically taken to be (km/s)/Mpc).3) To quote my thesis adviser misquoting Gertrude Stein, distant objects recede faster because “there’s more there there.”
Now, upon quick examination, Hubble’s Law seems to indicate that there is a distance, sufficiently large, at which the recession velocity exceeds the speed of light: [itex]d_H = c/H[/itex]. This is true, and, no, this is not in violation of anything you might think Einstein might have said. Yes, Einstein’s special theory of relativity constrains the motion of all massive objects to be slower than the speed of light. But how does that apply here? Are the points on our balloon moving? Yes, you can say they are — they are moving relative to each other on account of the balloon’s expansion. But you can also say that there is a sense in which they aren’t — they are at rest with respect to the balloon’s surface (the dots are drawn on there, fixed to the rubber surface). It is this latter situation, of motion relative to the dot’s local environment (its local inertial frame), that Einstein’s rule applies. So objects in the universe have two velocities: [itex]v_{\rm rec}[/itex], their recession velocity due to the expansion alone, and [itex]v_{\rm pec}[/itex], their peculiar velocity that accounts for motion relative to the expansion (from, for example, a rocket thrust). If we imagine a grid drawn on the balloon that expands along with the balloon, objects at rest with respect to this grid have an only recession, no peculiar velocity. But if objects move relative to this expanding grid4, part of their velocity is peculiar. In summary, [itex]v_{\rm tot}=v_{\rm rec}+v_{\rm pec}[/itex], and Einstein’s speed limit applies to the peculiar velocity (check out Figure 2).
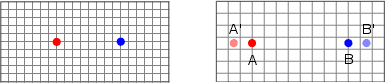
Fig. 2. Initially, the red and blue dot are separated by 8 units (left frame). After some expansion (right frame), [itex]A[/itex] and [itex]B[/itex] are still 8 units apart (although the units themselves have grown physically) — they have not moved relative to the expanding grid and so have [itex]v_{\rm pec} = 0[/itex]. After some amount of expansion, [itex]A'[/itex] and [itex]B'[/itex] have moved a bit relative to the expanding grid — this additional motion is due to nonzero [itex]v_{\rm pec}[/itex], so that their total relative velocity is composed of both [itex]v_{\rm rec}[/itex] from the expansion and [itex]v_{\rm pec}[/itex].
Cosmologists model the expansion of the universe with a single function, [itex]a(t)[/itex], called the scale factor (the expansion rate that we’ve been working with, [itex]H[/itex], is written in terms of [itex]a(t)[/itex] as [itex]H=\dot{a}/a[/itex] (where overdots denote time derivatives); it’s really a logarithmic rate of expansion). It describes the growth of length scales, [itex]x(t)[/itex], in an expanding universe: distances simply increase by an amount equal to the amount of expansion, [itex]x(t)\propto a(t)[/itex]. Look back at Figure 2. As the universe expands, the grid grows: the physical size of a tick mark increases. It still measures “1 unit”, so that today “1 unit” measures a greater physical distance than it did long ago. Units like this that grow with the expansion are called comoving, and they’re a handy tool in cosmology. In particular, anything that grows in scale along with the expansion has a constant comoving length, [itex]x_{\rm com}[/itex], while the physical length scale is [itex]x(t)=a(t)x_{\rm com}[/itex]. Comoving units are nice because they include the expansion in their definition: whether something is getting larger, smaller, or staying the same in comoving units tells us whether it’s increasing at a rate that is greater than, smaller than, or equal to the expansion. So, objects that recede along with the expansion ([itex]A[/itex] and [itex]B[/itex] in Figure 2) have [itex]v_{\rm pec}=0[/itex] and [itex]v_{\rm tot}=v_{\rm rec}[/itex]: their separation is constant in comoving units (8 units before and after the expansion). On the other hand, because [itex]A'[/itex] and [itex]B'[/itex] have peculiar velocity and move relative to the expanding grid, their separation is not constant in comoving units.
Superluminal recession and the Hubble sphere
So there is this interesting distance: [itex]d_H=c/H[/itex], at which objects appear to recede from Earth at the speed of light. It exists no matter the expansion rate: inflationary or otherwise. It’s called the Hubble distance, or Hubble radius, or Hubble scale. It is the radius of the Hubble sphere, bounding a region of space with Earth at the center. It might be supposed that it marks the edge of the observable universe — that it is the farthest distance out into the universe that we can presently see. After all, how do distant objects moving at speeds surpassing that of light emit light that has any hope of reaching us here on Earth?
Consider a galaxy located beyond the Hubble radius at a distance [itex]d_H[/itex] that emits a photon towards Earth. Of course, locally this photon is traveling at [itex]v_{\rm pec}=c[/itex] in accordance with special relativity. But, on account of the expansion, the photon is initially moving away from Earth with a speed [itex]v_{\rm tot}=v_{\rm rec}−c>0[/itex]5 (where positive velocities point away from Earth, in the direction of expansion.) Because this galaxy and the light it emits are being swept away from us by the expansion of space, it would indeed seem like this galaxy is forever unobservable. But that would be wrong. Many people make this mistake, including many cosmologists.6 The key is to examine how [itex]v_{\rm rec}[/itex] evolves in time. If [itex]H[/itex] is getting smaller in time — if the universe is slowing down in its expansion — then [itex]v_{\rm rec}[/itex] must decrease too because the recession velocity is due to the expansion. And, in the spirit of Hubble’s Law, the farther away from the object, the more rapid its deceleration! We can see this by obtaining an expression for [itex]\dot{v}_{\rm rec}[/itex] when [itex]H[/itex] is allowed to vary: [itex]\dot{v}_{\rm rec} = \dot{H}r+\dot{r}H[/itex], where [itex]\dot{H}[/itex] is the rate of change of the expansion rate. With [itex]\dot{r}=v_{\rm rec}=Hr[/itex], this becomes [itex]\dot{v}_{\rm rec}=r(\dot{H}+H^2)[/itex]. If we introduce something called the deceleration parameter, [itex]q=−(1+\dot{H}/H^2)[/itex], then we get something very much like Hubble’s Law, but for [itex]\dot{v}_{\rm rec}[/itex]:
[tex]\dot{v}_{\rm rec} = -H^2 q r.[/tex]
When the universe is decelerating, [itex]q>0[/itex], all objects decelerate: [itex]\dot{v}_{\rm rec}<0[/itex], in proportion to [itex]r[/itex]. So, what’s the big deal about [itex]v_{\rm rec}[/itex] getting smaller in a universe that is slowing down? Well, this means that the photon emitted by the galaxy with [itex]r>d_H[/itex], which we said earlier was moving away from us with a velocity [itex]v_{\rm rec}−c[/itex], is slowing down relative to Earth. When [itex]v_{\rm rec}[/itex] drops to [itex]c[/itex], the photon momentarily is moving neither toward nor away from us (it is locally moving at [itex]v_{\rm pec}=c[/itex] towards Earth but space is carrying it away at [itex]v_{\rm rec}=c[/itex], so [itex]v_{\rm tot}=c−c=0[/itex]). Once the recession velocity drops below [itex]c[/itex], the photon begins moving towards us at an ever-increasing rate (since now [itex]v_{\rm tot}=v_{\rm rec}−c<0[/itex] and [itex]v_{\rm rec}[/itex] is continuously decreasing making [itex]v_{\rm tot}[/itex] more and more negative). Eventually, it reaches Earth, [itex]v_{\rm rec}[/itex] goes to zero, and the photon whizzes into our telescope at the speed of light, [itex]c[/itex]! Meanwhile, the emitting galaxy could be well beyond the Hubble radius, receding at superluminal speeds. So superluminal recession of a light source is not, in itself, an impediment to our being able to observe this light. If the universe is decelerating, [itex]d_H[/itex] does not measure the size of the observable universe simply because all things must slow down.
We can understand this a different way by considering the motion of the Hubble radius itself, [itex]\dot{d}_H[/itex]. From the relation [itex]d_H=c/H[/itex], we get
[tex]\dot{d}_H=c(q+1),[/tex]
which says that when [itex]q>0[/itex], the Hubble sphere is racing away from us at a constant7 superluminal speed, [itex]\dot{d}_H>c[/itex]. Think about what this means. The Hubble radius marks the distance at which objects moving along with the expansion (comoving objects) recede with [itex]v_{\rm rec}=c[/itex]. This marker is itself moving faster than the speed limit it is directing (see Figure 3) with the result that the Hubble radius increases more quickly than length scales growing along with the expansion.
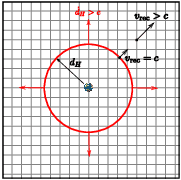
Fig. 3 The Hubble sphere moves away from Earth at superluminal speed, [itex]\dot{d}_H>c[/itex]. Meanwhile, objects moving along with the expansion recede from Earth with [itex]v_{\rm rec}=c[/itex] at [itex]d_H[/itex]. Inevitably, then, the Hubble sphere overtakes objects moving away with [itex]v_{\rm tot}<\dot{d}_H[/itex].
The result [itex]\dot{d}_H>c[/itex] is the hallmark of decelerated expansion — as the universe winds down, we must look farther out to find galaxies with superluminal recession speeds. This sequence of events is shown in Figure 4:
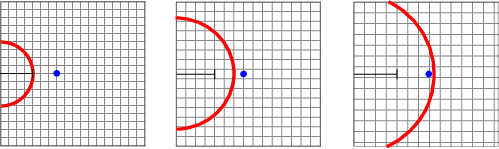
Fig. 4 Time sequence of the Hubble sphere (red circle) expanding to overtake a receding galaxy (blue dot) comoving with the expansion in a decelerating universe. A comoving length scale of 4 units is shown at each step for reference.
All of this can be summarized by observing that the comoving Hubble distance is increasing — its size according to the increasing tick marks is still increasing. This can be written concisely:
[tex]\dot{d}_{H,\rm com}=\frac{\rm d}{\rm dt}\frac{d_H}{a}=\frac{\dot{d}_H}{a}-\frac{d_H H}{a}=\frac{1}{a}(\dot{d}_H−c)=\frac{cq}{a}>0,[/tex]
where Eq. (2) has been used. Importantly, photons emitted by distant sources are not comoving objects: those emitted towards Earth have a smaller total velocity, [itex]v_{\rm tot}=v_{\rm rec}−c[/itex] (as discussed above, they have [itex]v_{\rm tot}=0[/itex] at the Hubble scale) than comoving objects at the same distance. Photons are therefore overtaken before their more quickly receding comoving sources. So Eq. (3) nicely summarizes the fate of superluminal objects in the decelerating universe: the comoving Hubble radius is growing and so all comoving objects will one day become visible.
The edge of the observable universe
We now know that we can see beyond the Hubble sphere, but just how far out can we look? Though evidently larger than the Hubble distance, the observable universe should have a finite size owing, if nothing else, to its finite age. The size of the observable universe is simply the distance that light could have traveled, from our location, since the big bang. Suppose we send a pulse of light outwards from our position at the dawn of time: in a static universe, it travels a distance [itex]D=ct[/itex], where [itex]t[/itex] is the age of the universe (around 13.8 billion years). In reality, though, the radius of the observable universe is closer to something like 46 billion lightyears. This apparent discrepancy is a common cause for confusion among the lay public and armchair cosmologists worldwide; creationists cite it as proof that cosmology is a fiction riddled with inconsistencies, cosmologists themselves either too stupid or too busy conspiring to take over the world to notice. That could all be true. But, really, we’ve simply neglected the effect of expansion on the flight of the photon. Take a look at Figure 5. The top row illustrates the static case: if the flight time is 13.8 billion years, then the distance traveled is simply 13.8 billion lightyears. The bottom row includes the effect of expansion: the expanding space “carries” the photon along with it. The photon is always traveling at [itex]c[/itex] locally, but as it recedes from us, it begins to pick up an additional recession velocity on account of the expansion in accordance with Hubble’s Law.

Fig. 5 A shell of photons emitted from our position marks the extent of the observable universe at the time. The top row depicts the progress of these photons as they move outwards in a static universe: after a time, [itex]t[/itex], they’ve gone a distance [itex]ct[/itex]. In the bottom row, the shell of photons now moves in an expanding universe. The expansion can be seen to help the photons along: the extra bit of distance gained in each time step over the static case is marked. Summing up all these extra bits yields a total distance greater than [itex]ct[/itex].
Recall that the speed of light in an expanding universe can be written as the sum of two parts: [itex]v_{\rm tot}=v_{\rm rec}+v_{\rm pec}[/itex]. Since [itex]v_{\rm rec}[/itex] is changing as the photon recedes (cf. Eq. (1)), we need to integrate [itex]v_{\rm tot}[/itex] from [itex]t=0[/itex] to the present to get the total distance traveled. This turns out to be a messy and clumsy calculation. An easier and conceptually more appealing approach is to consider the comoving distance that the photon travels, [itex]D_{\rm com}[/itex] (the physical distance in comoving coordinates). In the bottom row of Figure 5, for example, the comoving distance traveled by the photon is around 4.5 units (it begins at 4 units and ends at 8.5 units — remember a unit is a unit is a unit). What role does the expansion, through [itex]v_{\rm rec}[/itex], have in increasing the comoving distance, [itex]\dot{D}_{\rm com}[/itex]? None whatsoever, because [itex]v_{\rm rec}[/itex] is due to the expansion and comoving units include the expansion in their definition (recall Figure 2). The sole reason that the comoving distance changes in Figure 5 are that the photon is moving relative to the expansion (again, recall Figure 2). In essence, it is the [itex]v_{\rm pec}[/itex] that does all the work here8. While [itex]v_{\rm pec}=c[/itex], it steadily decreases when viewed in terms of comoving coordinates, [itex]c/a=\dot{D}_{\rm com}[/itex]: as the universe expands and the grid gets larger, the photon covers less ground according to this expanding grid. So the idea is to integrate [itex]c/a=\dot{D}_{\rm com}[/itex] from [itex]t=0[/itex] to the present, [itex]t_0[/itex], to obtain the comoving distance traveled by light since the big bang; to get the physical distance, we simply multiply by the scale factor (recall [itex]x=ax_{\rm com}[/itex]). This, then, is our integral:
[tex]D_{\rm com} =c\int_{0}^{t_0}\frac{{\rm d}t’}{a(t’)} = \frac{1}{q}\int_{0}^{t_0}{\rm d}d_{H,\rm com}.[/tex]
where we’ve made use of Eq. (3), giving [itex]D_{\rm com}(t_0)=q^{-1}d_{H,\rm com}(t_0)[/itex] (with [itex]d_{H,\rm com}=0[/itex] at the big bang, [itex]t=0[/itex]). This is a neat result that directly compares the sizes of the observable universe and the Hubble sphere. I’ve argued above that the former lies out beyond the latter: the truth of this statement all hinges on the size of the deceleration parameter, [itex]q[/itex]. In the decelerating universe, [itex]0<q\leq 1[/itex], and so [itex]D \geq d_H[/itex] with equality holding only for the case of a universe filled with nothing but light, where the expansion decelerates rapidly enough for the Hubble distance to increase at the same speed as the expanding shell of photons marking the edge of the observable universe. As the real universe contains more than just light (dust, planets, stars, teapots), that case is only of theoretical interest and for its entire history, the observable universe has stretched beyond the Hubble sphere, growing at a greater pace.
It may have struck you that we determined the size of the observable universe not by calculating the distance to the farthest objects that we can observe. This would amount to studying the flight of photons from these distant reaches to us here on Earth. We actually did the opposite — we studied the path of a photon emitted here on Earth out to the edge; in effect, we performed the correct calculation but for those who see us as the farthest object in their sky! Because the expansion of space is homogeneous and isotropic (uniform and the same in all directions), these two distances are actually the same, and so it doesn’t matter which we calculate. But, they do define two very different physical collections of events: those that we can influence and those that can influence us, within a given time frame.
We can actually draw this out. Figure 6 is a graph of distance, [itex]r[/itex], versus “time”, [itex]ct[/itex].9 We will assume a static space so as not to complicate things. Imagine that Earth is at [itex]r=0[/itex] and at [itex]t=0[/itex] we emit a photon out into space (black diagonal line in Figure 6).
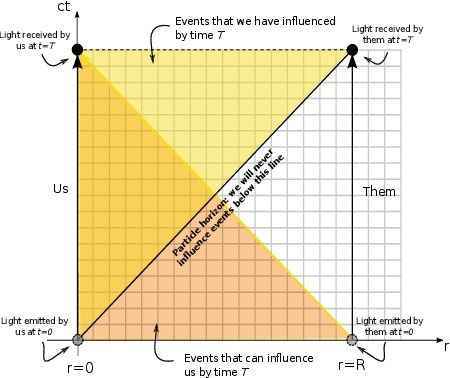
Fig. 6 [itex]r−ct[/itex] plane. Us at [itex]r=0[/itex] and a distant object (them), [itex]r=R[/itex]. We each emit a photon towards each other at [itex]t=0[/itex], and each receive it at [itex]t=T[/itex]. See text for details and discussion.
After a time T, it reaches a distant galaxy at [itex]r=R[/itex]. This is the distance we calculated for an expanding universe above, taking [itex]T[/itex] to be the present time. This photon path separates spacetime into two regions: those events that we have influenced (can reach with a light ray) by time T (the yellow wedge) and those that we will never influence — events that would require faster-than-light signals to affect (lines with slopes less than 1). These latter events exist in our past [itex]t<T[/itex], and so this boundary is known as the past event horizon. It is much more commonly (and perhaps confusingly) called the particle horizon. Notice that the yellow wedge does not represent the observable universe, which should comprise the collection of events that have influenced us (the photons coming from the distant reaches), which is instead given by the orange wedge. The boundary of the orange wedge is formed by the path of a photon emitted by the distant galaxy at [itex]t=0[/itex]; by the time it reaches us we have drifted ahead in time to [itex]T[/itex] (still, though at [itex]r=0[/itex] — we have not moved in space).10 This is a mirror image of the process of us sending a photon to them, and so even though the particle horizon does not bound the collection of observed events, it correctly yields its size.
Exit only: event horizons in the age of inflation
We have finally reached the main attraction: accelerated expansion. It is widely accepted that the universe underwent a period of ultra-rapid expansion in its earliest moments, driven by a mysterious, gravitationally-repulsive energy that inclined space to expand at an ever-increasing rate. This period of primordial inflation lasted but a cosmic heartbeat, but it had a profound influence on all that was to come after. Its consequences, in part, stem from the curious behavior of the Hubble sphere in an accelerating universe.
Let’s re-examine Eq. (1) for the case accelerated expansion, [itex]q<0[/itex]. We find, unsurprisingly, that [itex]\dot{v}_{\rm rec}>0[/itex]: objects receding with the expansion accelerate too. But, the rate of acceleration increases with [itex]r[/itex] so that as objects speed up in their recession, getting farther away, they continue to speed up, getting even farther away. A simple model of accelerated expansion occurs when [itex]H[/itex] is taken to be constant. But how can a constant expansion rate, [itex]H=\dot{a}/a[/itex], lead to accelerated expansion?
There is a slight abuse of terminology that pervades modern cosmology: the expansion rate, [itex]H[/itex], is really a logarithmic rate of expansion (I pointed this out earlier but with much less fanfare). A constant [itex]H[/itex] means that [itex]\dot{a}[/itex] increases in proportion to [itex]a(t)[/itex]: as the universe grows, so too must [itex]\dot{a}[/itex]. Let’s check this directly: since constant [itex]H[/itex] has [itex]\dot{H}=0[/itex], we have for the acceleration of the scale factor, [itex]\ddot{a}[/itex],
[tex]\frac{\ddot{a}}{a}=H^2>0.[/tex]
And, recognize that when [itex]\dot{a}[/itex] grows in proportion to [itex]a(t)[/itex], we have exponential growth of the scale factor: [itex]a(t)\propto e^{Ht}[/itex]. So when [itex]H[/itex] is constant, the universe expands exponentially, at an accelerated rate. This is called de Sitter expansion, and it corresponds to [itex]q=−1[/itex], the most negative [itex]q[/itex] that decency allows. It is really a special case, as accelerated expansion can be achieved even when [itex]H[/itex] varies as long as it doesn’t do so too quickly (these cases correspond to inflation in the range [itex]−1<q<0[/itex]).
What happens to the Hubble scale during inflation? With [itex]q<0[/itex], Eq. (2) gives [itex]\dot{d}_H<c[/itex]. The Hubble sphere grows more slowly than equidistant comoving objects (which are moving at [itex]c[/itex]), and so is overtaken by them. We therefore have a situation opposite to that shown in Figure 3: comoving length scales grow relative to the Hubble radius during inflation, [itex]\dot{d}_{H, \rm com} \propto \dot{d}_H−c<0[/itex] when [itex]\dot{d}_H<c[/itex]. We can say that the comoving Hubble distance is shrinking. Contrast Figure 7 with Figure 4.
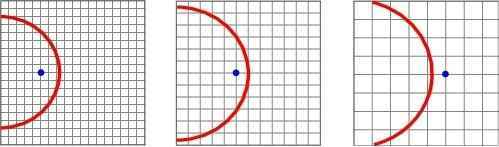
Fig. 7 Time sequence of the Hubble sphere (red circle) expanding in an inflating universe. The receding galaxy (blue dot), comoving with the expansion, is pulled outside the Hubble sphere.
What does this mean for our observable universe? In the decelerating universe, all objects eventually become visible simply because they are slowing down in their recession and the light they emit is able to find its way into our telescopes. Things are not so simple during inflation: it is easy to imagine a situation where the light emitted towards Earth by a distant galaxy gets overwhelmed by the accelerated expansion, dashing any hope of forward progress. Let’s test this by considering the path of a light ray emitted towards Earth when the universe is undergoing the most rapid expansion possible — de Sitter inflation. If the photon is emitted at a distance [itex]r[/itex] from Earth, its initial velocity is [itex]v_i=Hr−c[/itex]. As it strives against the expansion, it undergoes an acceleration [itex]a=H^2|q|r[/itex] away from Earth (this is Eq. (1)). The question is: given the expansion rate, [itex]H[/itex], what is the farthest distance from which we can receive light? We can solve this by applying conservation of energy to the equivalent kinematical problem of a particle moving against a repulsive force: [itex]v^2_f−v^2_i=2\int^r_0 a {\rm d}r’=H^2r^2[/itex], where [itex]H[/itex] is constant and [itex]q=−1[/itex] during de Sitter expansion. Since Earth is at [itex]r=0[/itex], [itex]v_f=−c[/itex] (recall that negative velocities point opposite the expansion) and we find [itex]r=d_H[/itex]: photons emitted at the Hubble scale will just reach Earth. Photons emitted by objects with [itex]r>d_H[/itex] won’t ever make it — though moving locally at the speed of light, the intervening space is expanding so rapidly that the photons simply don’t gain ground. It is like trying to run on a treadmill that is rolling by too fast.
We can reason further that when the magnitude of the accelerated expansion is not as great as de Sitter (when [itex]−1<q<0[/itex]), objects beyond the Hubble scale are visible out to a distance determined by [itex]q[/itex], but only for a while: as long as there is accelerated expansion of any kind, there will be a distance beyond which we will not receive any light.
We can study this important distance more carefully by recalling the symmetry of ingoing and outgoing light: if we cannot receive light from a distant galaxy here on Earth, then they likewise cannot receive light from us, no matter how long they wait. Just as we used Eq. (4) to see how far light has traveled since the big bang, with a slight change in integration limits we can use it to find out how far light emitted today from Earth will travel into the future. If what we’ve learned above is correct, this comoving distance should be finite:
[tex]\ell_{\rm com}=c\int^\infty_{t_0} \frac{{\rm d}t’}{a(t’)}=\int^\infty_{t_0}\frac{{\rm d}d_{H,\rm com}}{q},[/tex]
where the limits of integration run from today, [itex]t_0[/itex], to the infinite future. We emphasize that this is a comoving distance — the physical distance that a photon moves in an infinite amount of time is of course infinite. Instead, what this result says is that there is a point that is comoving with the expansion that will always keep ahead of a photon emitted today from Earth.
If we assume for the sake of demonstration that [itex]q[/itex] is constant (it’s only truly constant for [itex]q=−1[/itex]), then we find [itex]\ell_{\rm com}=q^{−1}(d_{H,\rm com}(\infty)−d_{H,\rm com}(t_0))=−q^{−1}d_{H,\rm com}(t_0)[/itex], where [itex]\lim_{t\rightarrow \infty}d_{H,\rm com}(t)=d_H(t)/a(t)=0[/itex] because [itex]a(t)[/itex] goes to infinity more quickly than [itex]d_H(t)[/itex]. So, during de Sitter inflation for example, the comoving distance, [itex]\ell_{\rm com}[/itex], is determined by the comoving Hubble radius: objects at [itex]d_H[/itex] and beyond that recede along with the expansion are forever out of reach (see Figure 9).
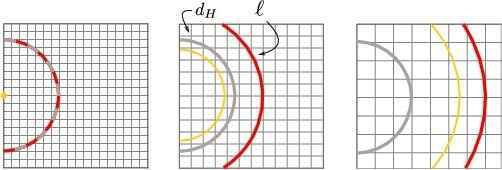
Fig. 9 Illustration of the event horizon, [itex]\ell[/itex], during de Sitter expansion. The gray circle is the Hubble sphere and the red circle is the event horizon. The leftmost frame is today: a photon is just emitted (yellow dot), the Hubble sphere and event horizon coincide. Subsequent frames showtimes in the future, as the shell of photons moves outwards. The Hubble sphere does not expand since [itex]\dot{d}_H=0[/itex] during de Sitter expansion. The event horizon, the comoving distance (7 units) that coincides with the Hubble scale today (leftmost frame), moves outwards with the expansion. Even if we included many more frames into the future, the photons never reach the receding event horizon.
The boundary set by [itex]\ell[/itex] carves out a region of spacetime containing events that will never influence us: those events beyond [itex]\ell[/itex] occurring now and forever into the future. For this reason, [itex]\ell[/itex] is known as our future event horizon, or simply, our event horizon. Contrast this with the particle horizon, our past event horizon, consisting of those events we will never influence (cf. Figure 6 and surrounding discussion). We can draw something like Figure 6 to depict the event horizon, but we can’t ignore the expansion because the event horizon exists only by virtue of the inflating space.11 We can include the expansion by using comoving spatial coordinates, [itex]r_{\rm com}=r/a[/itex]. But we have the additional issue of taking time to infinity on a finite (and relatively small) sheet of paper.
We evidently need a new time variable: it’s not initially obvious why this helps, but consider conformal time, [itex]{\rm d}\tau={\rm d}t/a(t)[/itex]. This is like having a watch that slows down as the universe expands. For the case of de Sitter expansion, the scale factor grows exponentially in time, [itex]a(t)\sim e^{Ht}[/itex], so that [itex]\tau=−(aH)^{−1}[/itex], where the integration constant has been chosen so that [itex]\tau(t\rightarrow \infty)=0[/itex]. Notice that [itex]\tau[/itex] is negative, running from [itex]-\infty[/itex] to zero. This switch to conformal time brings the infinite future [itex](t \rightarrow \infty)[/itex] to a finite value, [itex]\tau=0[/itex] (although it comes at a cost: [itex]t=0[/itex], which was the finite beginning of the universe, gets pushed out to [itex]\tau=−\infty[/itex]. This is okay, though, since we aren’t going to dwell on the past.)
If we work in terms of conformal time, [itex]\tau[/itex], and comoving spatial coordinate, [itex]r_{\rm com}=r/a[/itex], we can devise a spacetime diagram for the case of de Sitter inflation that takes the expansion into account and fits on the page, Figure 10. We again consider the same two light rays, but notice that this time the light ray emitted by the distant galaxy at [itex]r_{\rm com}=R[/itex] and [itex]\tau=−\mathcal{T}[/itex] is the last one we will ever receive. Those emitted later than [itex]\tau=−\mathcal{T}[/itex] by this galaxy won’t reach us before the infinite future is reached, [itex]\tau=0[/itex]. Yes, this talk of “reaching” infinity is silly — working with conformal time does that to you. What we mean is simply that those light rays that are emitted from [itex]r_{\rm com}=R[/itex] after [itex]t(−\mathcal{T})=T[/itex] will never reach us, no matter how long we wait. The boundary, then, separating the collection of events that do eventually influence us and those that never will is the event horizon. This is what’s so special about inflation — it is a dynamical process by which causal objects become acausal.
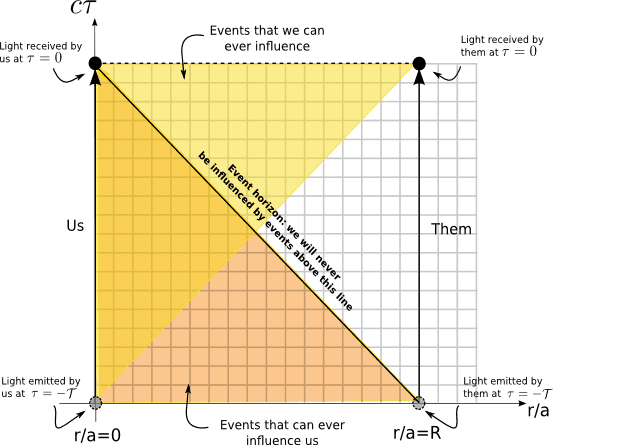
Fig. 10 [itex]r_{\rm com}−c\tau[/itex] plane. Us [itex]r=0[/itex] and a distant object (them), [itex]r=R[/itex]. The last light signal that we will ever receive is emitted by them at [itex]\tau=−\mathcal{T}[/itex]. The infinite future lies on the line [itex]\tau=0[/itex]. See text for details and discussion.
The accelerated expansion “pushes” all comoving objects outwards towards the event horizon, a conveyor belt to the point of no return. What all of this means, of course, is that the inflating universe is a rather lonely place. But, while the accelerated expansion acts to dilute the observable universe during inflation, we eventually rediscover stuff that was pushed beyond [itex]\ell[/itex] when inflation ends and the universe decelerates in its expansion. After inflation, the Hubble scale begins to race ahead faster than comoving lengths scales and the distant, causally dislocated regions become visible again. This is why it is possible to observe “superhorizon”-scale correlations in the cosmic microwave background, but that’s a story for another time.
In conclusion, we have hopefully learned a few things. 1) Expansion does not a have speed, so we don’t say that the universe expands at this or that speed. 2) Objects in space do have speeds, and it is possible for these speeds to exceed that of light. This is a consequence of an expanding universe, is not unique to inflation, and doesn’t bother Prof. Einstein. 3) Objects that are currently receding at superluminal velocities are nonetheless observable (the exceptional case of de Sitter inflation notwithstanding, but it’s not just because the objects are moving faster than [itex]c[/itex]!). 4) The observable universe is larger than the age of the universe times the speed of light because the expansion increases the distance that light has traveled since the big bang. This distance is called the particle horizon. 5) During inflation objects accelerate without bound, eventually losing causal contact with Earth. This happens when the objects attain recession speeds great enough that the light they emit in the direction of Earth has a net velocity away from us. These recession speeds occur at a special distance called the event horizon: all goings-on outside the event horizon is forever hidden from us.
References and Footnotes
[1] T.M. Davis and C.H. Lineweaver, “Expanding confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe,” Submitted to: Proc.Astron.Soc.Austral. [astro-ph/0310808]
1More correctly, there is no inside of the balloon geometrically — it is an artifact of constructing a sphere in three-dimensional space. Surprisingly, we could construct just as good of a sphere in only two dimensions. back
2Decline also urges to associate space with any sort of substance with elastic properties like rubber. back
3Mpc is a megaparsec — a unit of distance equivalent to 3.26 million lightyears, not a unit of time used to clock the Kessel Run. back
4All this talk of background grids smacks of Newton’s absolute space, doesn’t it? Fear not though, the background grid is really just some rest frame. The cosmic microwave background happens to provide a suitable rest frame in practice. back
5In the cosmological setting, we get to add the velocities of photons as in Galilean relativity, just like any other old classical object. back
6I, too, thought this way until I was set straight by Davis and Lineweaver [1]. back
7The Hubble radius is not a physical object receding with the expansion, so we don’t apply Hubble’s Law to it. back
8Yes, I just said that the reason for the 46Gly distance was that the expansion was important. It is! When working in comoving coordinates, however, we repackage the effects of the expansion into [itex]v_{\rm pec}[/itex]. back
9I could make this the usual time, [itex]t[/itex], but then from the equation [itex]r=ct[/itex], the path of light in the plane would have an insanely steep slope because [itex]c[/itex] is so large. Using the “time” [itex]ct[/itex] effectively rescales the time coordinate so that light has a speed (and its path has a slope ) of 1 on this graph. back
10The particle horizon exists because the universe has a finite age; the big bang occurs throughout space at a moment in time (corresponding to the line, [itex]t=0[/itex] in Figure 6). This spacelike singularity is a far cry from the popular misconception of the big bang as a localized explosion occurring in a pre-existing space. back
11We ignored the expansion in Figure 6 because particle horizons are qualitatively similar in static and decelerating spaces. back
After a brief stint as a cosmologist, I wound up at the interface of data science and cybersecurity, thinking about ways of applying machine learning and big data analytics to detect cyber attacks. I still enjoy thinking and learning about the universe, and Physics Forums has been a great way to stay engaged. I like to read and write about science, computers, and sometimes, against my better judgment, philosophy. I like beer, cats, books, and one spectacular woman who puts up with my tomfoolery.







Leave a Reply
Want to join the discussion?Feel free to contribute!