Learn Why Ohm’s Law Is Not a Law
At first, I wanted this title to say “Ohm’s law is not a Law.” But someone else used that phrase in a recent PF thread, and a storm of protest followed. We are talking about the relationship between Voltage between two points in a circuit and the current between those same two points.
##R=V/I##, or ##V=IR##, or ##I=V/R##
I won’t explicitly talk about inductance or capacitance, or AC impedances, although all of those could substitute for ##R## in the following discussion.
Table of Contents
Semantics
Newton’s Second Law can be derived from fundamental symmetries in nature. But Ohm’s law is not derived, it was empirically discovered by Georg Ohm. He found materials that have a linear relationship of voltage to current within a specified range are called “ohmic.” Many useful materials and useful electric devices are non-ohmic.
Beginners often believe that there is great significance in the use of words like “law” or “theory” In physics. Not so. Often it is just an accident of history or a phrase that slides easily off the tongue. It could have been called Ohm’s rule or Ohm’s observation, but it wasn’t.
Underlying Assumptions and Limitations
Really there is only one assumption behind Ohm’s law; linearity. Not in the mathematical sense, but rather a graph of voltage versus current shows an approximately straight line in a given range.
There are always limits to the range even though they may not be explicitly mentioned. For example, at high voltages breakdown and arcing can occur. At high currents, things tend to melt. In the old days, we said that real-world resistance can not be zero. But now we know that superconductors are an exception to that rule. ##R=0## is OK for superconductors.
Students often forget that limits exist. A frequent (and annoying) student question is, “So if ##I=V/R##, what happens when ##R=0##. Haha, LOL.” They think that disproves the “law” and thus diminishes the credibility of science in general. Their logic is false.
Ohm’s law Has Several Forms
##I=V/R## may be the most familiar form of Ohm’s law, but it is far from the only one.
- In AC analysis, we use ##\bar V=\bar I\bar Z##, where ##\bar V##, ##\bar I## and ##\bar Z## are all complex vectors. ##\bar Z## is the complex impedance that can describe combinations of resistance, inductance, and capacitance, without differential equations. See PF Insights AC Power Analysis, Part 1 Basics.
- ##\overrightarrow E=\rho \overrightarrow J## is the continuous form of Ohm’s law. where ##\overrightarrow E## is the electric field vector with units of volts per meter (analogous to ##V## of Ohm’s law which has units of volts), ##\overrightarrow J## is the current density vector with units of amperes per unit area (analogous to ##I## of Ohm’s law which has units of amperes), and ##\rho## is the resistivity with units of ohm·meters. Use this form to model currents in 3-dimensional space.
- If an external ##B##-field is present and the conductor is not at rest but moving at velocity ##v##, then we use: ##(\overrightarrow E + v \times \overrightarrow B)=\rho \overrightarrow J##
- There are also variants of Ohm’s law for 2 D sheets, for magnetic circuits (Hopkinson’s Law), Frick’s Law for diffusion-dominated cases, and for semiconductors.
Someone on PF once said that one form was the only “true” Ohm’s law. I disagree. All the forms are useful in different contexts. We can honor Georg Ohm by using his name to cover all the variants, even if he didn’t personally invent all of them.
Real-Life Example, A Solar Panel
A solar panel is a real-life device. Below, we see a family of curves showing the Voltage V versus current I relationship of a solar panel. Each curve represents a different value of solar intensity. As you can see, the curves range from nearly an ideal voltage source (vertical) to a nearly ideal current source (horizontal), to everything in between.
We can draw straight line segments to define the average resistance over a particular range, like R1, R2 or R3. As you can see, the panel ranges from nearly an ideal voltage source to a nearly ideal current source, to everything in between. R4 shows a resistance defined by the tangent to the curve at one particular point. I call R4 the resistance linearized about a point on the curve.
We could use these resistances, plus a Thevanin’s Equivalent voltage ##V_{thev}## to model the solar panel in a circuit to be solved using Ohm’s law. (##V_{thev}## is the place where the straight line intercepts the ##V## axis or where ##I=0##).
Arbitrary Numbers of Arbitrary Electric Devices
When we go beyond a simple resistor made of some material with a linear V-I relationship, we find that very many real-world devices are non-linear. For example, the constant power device (yellow) and the tunnel diode device (blue) curves seen below. There are no physical constraints on the shape of a V-I relationship other than that both V and I must be finite. Even a multi-valued curve that loops back on itself violates no physical law.
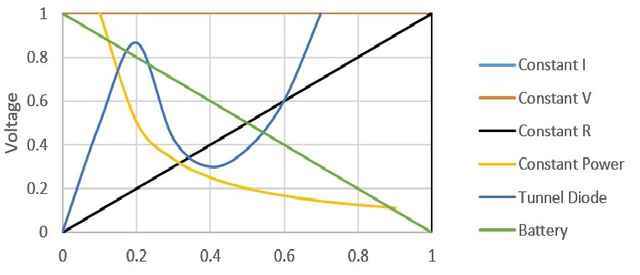
Students in elementary circuits courses often learn 0nly about the constant R (i.e. the resistor) element, plus L and C. Other kinds of nonlinear circuit devices may not even be mentioned.
At first glance, you might say that Ohm’s law doesn’t apply to nonlinear devices, but that’s not true. Suppose we had a circuit containing a solar panel, a constant power, and a tunnel diode. A student using paper and pencil could not be asked to solve such a circuit, so courses that limit themselves to paper and pencil methods do not cover nonlinear elements. But using computers, there is a relatively simple method:
- Guess an initial V and I point along the curve for each device.
- Find the linearized resistance (analogous to R4) for each device at the V and I guess point.
- Solve the linearized circuit using Ohm’s law, calculating new values for each V and I.
- Use the calculated V and I as the new guess and return to step 2.
An iteration like that is very easy to perform with a computer. It isn’t guaranteed to succeed, but when it does succeed, after several passes through steps 2 and 3, it will calculate values for V and I that simultaneously satisfy the relationships of all linear and nonlinear elements in the circuit. It is routine in power grid analysis to solve circuits with a million or more diverse nonlinear elements. Thus, even when modeling devices that don’t seem to obey Ohm’s law, that we can make productive use of Ohm’s law nevertheless. I’ll say it again using stronger words. Ohm’s law cannot be violated in real life; rather it can be adapted to nearly all real-life situations in electric circuits.
Ohm’s law is not always a complete description of electrical devices, but Ohm’s law is almost always a useful tool. Students are advised to learn to think that way. Physicists and engineers seek usefulness and try to leave the truth to philosophers.
Electricity Study Levels
One can study and explain electricity at (at least) 5 levels.
- Quantum Electrodynamics (QED)
- Maxwell’s Equations
- The Drude Model
- Circuit Analysis
- RF circuits and propagation
In this article, my focus was circuit analysis. One of the standard assumptions for circuit analysis is that Kirchoffs laws apply instantaneously to the entire circuit. That makes ##V## ##I## and ##R## co-equal partners. None of the three can be said to because and the other effect. All three apply simultaneously.
Students dissatisfied with Circuit Analysis sometimes yearn for physical explanations and invent false narratives about what happens first and what comes next. If you are such a student, I urge you to study Circuit Analysis first, then follow up with the other levels. If that describes you, I advise that the next step is to abandon circuit analysis, Ohm’s law, Kirchoff’s laws, and to learn Maxwell’s equation as the next deeper step. Fields, not electron motion are the key to the next deeper step.
—
Thanks to PF regular @Jim Hardy for his assistance.
Dick Mills is a retired analytical power engineer. Power plant training simulators, power system analysis software, fault-tree analysis, nuclear fuel management, process optimization, power grid operations, and the integration of energy markets into operation software, were his fields. All those things were analytical. None of them were hands-on.
Dick has also been an exterminator, a fire fighter, an airplane and glider pilot, a carney, and an active toastmaster.
During the years 2005-2017. Dick lived and cruised full-time aboard the sailing vessel Tarwathie (see my avatar picture). That was very hands on. During that time, Dick became a student of Leonard Susskind and a physics buff. Dick’s blog (no longer active) is at dickandlibby.blogspot.com, there are more than 2700 articles on that blog relating the the cruising life.







Leave a Reply
Want to join the discussion?Feel free to contribute!