- #1
Mr Beatnik
- 8
- 0
Homework Statement
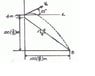
Ok forgive me as an engineering student but this problem should be easier than it seems. The Problem: It is observed that the skier leaves the ramp A at an angle (Theata=25 degrees) with the horizontal. If he strikes the ground at point B, determine his initial speed,V, and the time of flight,t.
Homework Equations
I have used:
s=vt
s=s+vt+1/2at^2
The dimensions needed are correct and are 100m down the slope alligned, the ramp he leaves from is 4m high and the ramp is angled at a 3,4,5 triangle.
This problem is 12-110 from the Hibbeler Dynamics 12th edition
The Attempt at a Solution
I have setup the equations as
(1) 100(4/5)=Vcos(25)t
(2) -4-100(3/5)=0+Vsin(25)t+(1/2)(-9.81)t^2
I have tried solving (1) for t and plugging in into (2) but come out with a strange decimal and also solving (1) for V and plugging into (2) I can't seem to get it.
I know the answers are supposed to be: V=19.4m/s t=4.54s
Please help!