- #1
ttback
- 4
- 0
There is a set of two problems, I can solve problem 1, can't solve problem 2. But in order for you to help me solving problem 2, I think you need to use the answer for problem 1.
P1. A satellite hovers over a certain spot on the equator of (rotating) Earth.
What is the altitude of its orbit(called a geosynchronous orbit)
We use Kepler's Law of Period to get r, which is the distance between the satellite and the center of Earth.
T^2 = (4*pi^2 / G * Me) r^3
T = Time of one day = 24 h = 86400 s
Me = 5.98 x 10^24 kg
G = 6.67 x 10^-11 (some crazy unit)
r = That is the unknown we want
Altitude = r - Re
r = 4.225 x 10^7
Re = 6.37 x 10^6 m
Altitude = r - Re = 3.58 x 10^7 m
================================================================
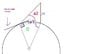
P2. Assume that the satellite of P1 is in orbit at the longitude of Chicago. You are in Chicago (latitude 47.5 degree) and want to pick up the signals the satellite broadcasts. In what direction should you point antenna?
The situation in the problem, as I interpret, is that the satellite is now on the same longitude as Chicago, same latitude as equator, and still hovering over one fixed point on the equator.
If so, the antenna must turn to the south and makes a angle with the ground to point at the satellite.
Now I know the satellite's altitude from P1, I can also find out the distance between Chicago and the Equator,(from the latitude) then I can calculate the angle using Arctan(Altitude/Distance).
But my question is, isn't Earth round? So the distance between Chicago and that Equator was measured by a curved path? Then we wouldn't really have a triangle, right?
Can we still use Arctan() to solve this problem? Or maybe I am just overthinking because the curve can be ignored?
Homework Statement
P1. A satellite hovers over a certain spot on the equator of (rotating) Earth.
What is the altitude of its orbit(called a geosynchronous orbit)
Homework Equations
We use Kepler's Law of Period to get r, which is the distance between the satellite and the center of Earth.
T^2 = (4*pi^2 / G * Me) r^3
T = Time of one day = 24 h = 86400 s
Me = 5.98 x 10^24 kg
G = 6.67 x 10^-11 (some crazy unit)
r = That is the unknown we want
The Attempt at a Solution
Altitude = r - Re
r = 4.225 x 10^7
Re = 6.37 x 10^6 m
Altitude = r - Re = 3.58 x 10^7 m
================================================================
P2. Assume that the satellite of P1 is in orbit at the longitude of Chicago. You are in Chicago (latitude 47.5 degree) and want to pick up the signals the satellite broadcasts. In what direction should you point antenna?
The situation in the problem, as I interpret, is that the satellite is now on the same longitude as Chicago, same latitude as equator, and still hovering over one fixed point on the equator.
If so, the antenna must turn to the south and makes a angle with the ground to point at the satellite.
Now I know the satellite's altitude from P1, I can also find out the distance between Chicago and the Equator,(from the latitude) then I can calculate the angle using Arctan(Altitude/Distance).
But my question is, isn't Earth round? So the distance between Chicago and that Equator was measured by a curved path? Then we wouldn't really have a triangle, right?
Can we still use Arctan() to solve this problem? Or maybe I am just overthinking because the curve can be ignored?