- #1
sapiental
- 118
- 0
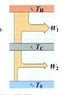
Consider a Carnot engine operating between temperatures T_h_ and T_c_, where T_c_ is above the ambient temperature T_o_. A second engine operates between the temperatures T_c_ and T_o_.
Calculate (in terms of temperatures) the overall efficiency of the two-stage engine operating this way, and compare with the efficiency of a single Carnot engine operating between the high and low temperatures T_h_ and T_o_.
Which has the higher efficiency, the two-stage or the single engine?
e = 1 - (T_c_/T_h_)
e_2stage_ = 1 - (T_c_/T_h_)(T_o_/T_c_) = 1 - (T_h_-T_o_)/(T_h_)
If I set this up correctly, the 2tage carnot engine will be by far more efficent since it uses the discarded heat to create more work.
I have a funny feeling as if this is violating some law of thermodynamics however..
any advice and feedback is much appreciated.
Thanks.
Calculate (in terms of temperatures) the overall efficiency of the two-stage engine operating this way, and compare with the efficiency of a single Carnot engine operating between the high and low temperatures T_h_ and T_o_.
Which has the higher efficiency, the two-stage or the single engine?
e = 1 - (T_c_/T_h_)
e_2stage_ = 1 - (T_c_/T_h_)(T_o_/T_c_) = 1 - (T_h_-T_o_)/(T_h_)
If I set this up correctly, the 2tage carnot engine will be by far more efficent since it uses the discarded heat to create more work.
I have a funny feeling as if this is violating some law of thermodynamics however..
any advice and feedback is much appreciated.
Thanks.