2D Finite Difference Convergence Rate Issues

[Aggie1313]

I have completed a 2D finite difference code in MATLAB that has a domain of (0,1)x(0,1) and has Dirichlet Boundary Conditions of value zero along the boundary. I get convergence rates of 2 for second order and 4 for fourth order. My issue now is that I'm now wanting to change the domain to a more complex domain and see the resulting convergence rates. I have cut 4 square holes throughout the plate within the domain (0,1)x(0,1) with Dirichlet Boundary Conditions of value zero. When I run the code for the new domain I do not get convergence rates of 2 and 4. They usually end up being in the 1.3 - 2 range. I'm imposing the inner boundary conditions using the penalty method.

It is my belief that the holes within the new domain are causing the convergence rates to change. Is there a reason for this or is something just incorrect in my calculations? I have made sure the code was correct using the method of manufactured solutions.

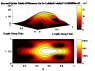
Attached is example domain and solution output.

I can attach the code if needed but I'm more so asking a theory question I suppose

 

[gtoguy97]

.It is likely that the holes in the domain are causing the convergence rate to change. This could be due to the penalty method you are using to impose the inner boundary conditions, which may not be accurate enough to capture the correct solution. For example, the penalty method assumes a linear relationship between the solution values at the inner boundary and outside the boundary, and this assumption may not hold for the complex domain with the holes. You can try different methods for imposing the inner boundary conditions to see if the convergence rates improve. Alternatively, you can increase the resolution of the grid or use higher-order discretization schemes to ensure accuracy.