- #1
Sirsh
- 267
- 10
Hi there,
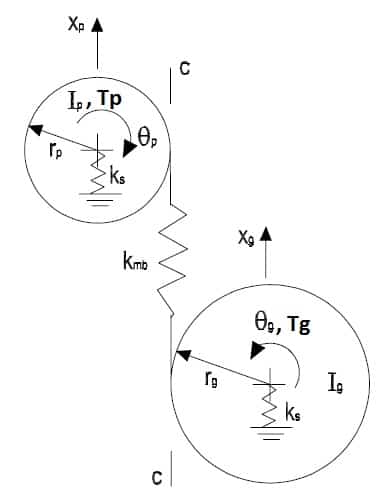
I am modelling a four degree of freedom system which is the dynamics of two spur gears in mesh, having two rotational and two translation degrees of freedom, respectively, a diagram exhibiting the system can be seen below.
I have derived the equations of motion (EOM) and rearranged into ODEs as seen:
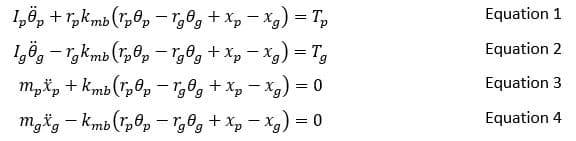
Where the force and torque relations are (used in the derivation process):
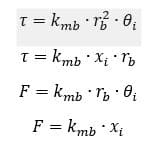
Following this I have made rewritten equations 1-4 into matrix form, creating mass and stiffness matrices.
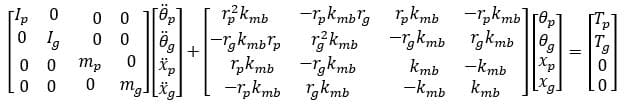
I have been having trouble achieving steady state of this system in my simulations using Simulink and MATLAB, so I was advised to check the eigenvalues of the dynamic matrix as well as make sure that the mass matrix is diagonal while the stiffness matrix is symmetrical - they both are.
The dynamic matrix is defined as the inverse of the mass matrix multiplied by the stiffness matrix, e.g. Dyn = inv(M)*K.
Now, I have input all this into MATLAB with the corresponding values for each of the parameters. However, I can never achieve purely positive eigenvalues for this system, as I'm told is required and may be the issue with my simulation, and where if they're not all positive (including one zero) then the system of equations are incorrect. However, I have reviewed literature on spur gear dynamics and the equations are the same...
This is exhibited below as an output of my MATLAB eigenvalue calculating script:

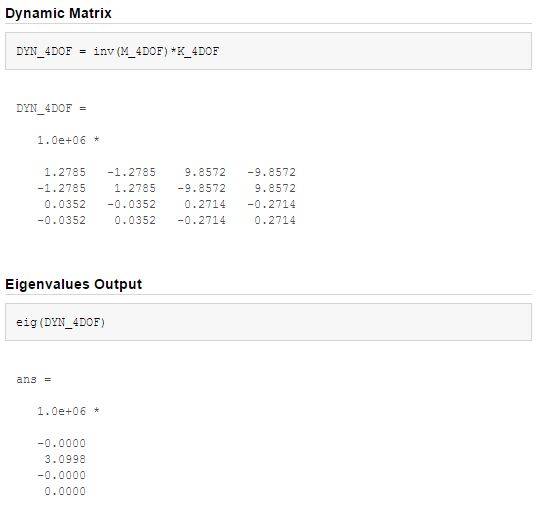
Any help would be appreciated greatly, as I am an undergraduate student researching solo. So any advice on my interpretation of either the system dynamics or eigenvalue interpretation would be helpful from you all.
Thanks, Sirsh.
I am modelling a four degree of freedom system which is the dynamics of two spur gears in mesh, having two rotational and two translation degrees of freedom, respectively, a diagram exhibiting the system can be seen below.
I have derived the equations of motion (EOM) and rearranged into ODEs as seen:
Where the force and torque relations are (used in the derivation process):
Following this I have made rewritten equations 1-4 into matrix form, creating mass and stiffness matrices.
I have been having trouble achieving steady state of this system in my simulations using Simulink and MATLAB, so I was advised to check the eigenvalues of the dynamic matrix as well as make sure that the mass matrix is diagonal while the stiffness matrix is symmetrical - they both are.
The dynamic matrix is defined as the inverse of the mass matrix multiplied by the stiffness matrix, e.g. Dyn = inv(M)*K.
Now, I have input all this into MATLAB with the corresponding values for each of the parameters. However, I can never achieve purely positive eigenvalues for this system, as I'm told is required and may be the issue with my simulation, and where if they're not all positive (including one zero) then the system of equations are incorrect. However, I have reviewed literature on spur gear dynamics and the equations are the same...
This is exhibited below as an output of my MATLAB eigenvalue calculating script:
Any help would be appreciated greatly, as I am an undergraduate student researching solo. So any advice on my interpretation of either the system dynamics or eigenvalue interpretation would be helpful from you all.
Thanks, Sirsh.