- #1
Winzer
- 598
- 0
Homework Statement
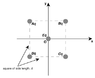
Four charges, Aq, Bq, Cq, and Dq (where q = 3.50 ×10−7 C), sit in a plane at the corners of a square whose sides have length d = 23.5 cm, as shown in the diagram below. A charge, Eq, is placed at the origin at the center of the square. (Note that A, B, C, D, and E are integer multipliers.)
DATA: A = 2, B = 4, C = 5, D = 8, E = 1. Consider the charge at the center of the square, Eq.
What is the net y-component of the force on this charge?
Consider the situation where A=B=C=D=1, E=-1, and the following statements. Select "True" or "False" for each statement.
1) The sum of the forces on the center charge in the y-direction equals zero.
2)If one were to triple the magnitude of the negative charge, the negative charge would be in equilibrium.
3)The equilibrium point at the center is a stable equilibrium for the motion of the negative charge in the plane of the square.
4)The sum of the forces on the center charge in the x-direction does not equal zero.
5)If one were to double the magnitude of the upper-right-hand positive charge, the negative charge would be in equilibrium.
6)The equilibrium point at the center is an unstable equilibrium for the motion of the negative charge in the line from the center charge and perpendicular to the plane of the square.
Homework Equations
[tex] F= \frac{Kq_{1}q_{2}}{r^2}[/tex]
The Attempt at a Solution
So for the first one I break up each each force acting on E. I then do [tex]Fsin(\theta)=F_{y}[/tex] for each one and take the sum right, i keep getting it wrong for some reason.
For the second part:
1)T
2)T
3)T
4)F
5)F
6)F
Thanks
Attachments
Last edited: