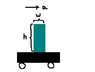- #1
RedAlert
- 23
- 0
Hey guys, I'm struggling a little bit with this physics problem (look at the attachment for a diagram of the situation about to outline).
There is a cart, upon which a block of a material of uniform density, with width w and height h rests. The coefficient of friction between the block and the cart is enough so that when the cart begins to accelerate, the block cannot slide, but instead topples over.
At what acceleration will the block topple? I need to find a general solution for this situation.
These are the forces I can identify:
a) the weight of the block, mg (acting through the center of mass, which lays in the geometric center of the object, since it is of uniform density)
b) the normal force to the weight of the block (acting through the center of mass, in the direction opposite to that of mg)
c) the force of friction between the block and cart (this is the force that is accelerating the cart, and it acts along the surface of the block)
The problem is, I can't figure out which force causes the counterclockwise torque that causes the block to topple over, and I know for a fact it's not one of the above three forces. I know it's a counterclockwise torque because I did some modelling using a sheet of paper and an eraser, which acted as my block). Our teacher says that the force responsible for the torque would be the "pseudo force", ma, which acts in the direction parallel to the acceleration, a, and through the center of mass.
That doesn't make sense either, because that force, ma, would cause a torque in the clockwise direction, not counterclockwise.
WTH is happening?
Also, I learned that any force going through the center of mass of an object, cannot create a torque. Why then, do we use mg (the weight of an object), in torque analyses often times?
Your help is greatly appreciated. :)
There is a cart, upon which a block of a material of uniform density, with width w and height h rests. The coefficient of friction between the block and the cart is enough so that when the cart begins to accelerate, the block cannot slide, but instead topples over.
At what acceleration will the block topple? I need to find a general solution for this situation.
These are the forces I can identify:
a) the weight of the block, mg (acting through the center of mass, which lays in the geometric center of the object, since it is of uniform density)
b) the normal force to the weight of the block (acting through the center of mass, in the direction opposite to that of mg)
c) the force of friction between the block and cart (this is the force that is accelerating the cart, and it acts along the surface of the block)
The problem is, I can't figure out which force causes the counterclockwise torque that causes the block to topple over, and I know for a fact it's not one of the above three forces. I know it's a counterclockwise torque because I did some modelling using a sheet of paper and an eraser, which acted as my block). Our teacher says that the force responsible for the torque would be the "pseudo force", ma, which acts in the direction parallel to the acceleration, a, and through the center of mass.
That doesn't make sense either, because that force, ma, would cause a torque in the clockwise direction, not counterclockwise.
WTH is happening?
Also, I learned that any force going through the center of mass of an object, cannot create a torque. Why then, do we use mg (the weight of an object), in torque analyses often times?
Your help is greatly appreciated. :)
Attachments
Last edited: