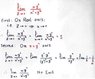- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Limited Value in Compound Functions: Remembering Number Paths
- Thread starter m_s_a
- Start date
In summary: What have derivatives got to do with it? You were posting limit problems. Or something. I give up. I don't know what your question or problem is.I support the second solution
Physics news on Phys.org
- #2
Dick
Science Advisor
Homework Helper
- 26,259
- 623
We remember that we in back of path from not a limited from the numbers. Is that wrong? I really can't understand you. Sorry.
- #3
- #4
Dick
Science Advisor
Homework Helper
- 26,259
- 623
m_s_a said:He is not at the end a presence
Why ؟
The previous way the others is suitable ? why ?...
Look please:
I will. When it's approved. I think that gives me time to get a good night's sleep.
- #5
Dick
Science Advisor
Homework Helper
- 26,259
- 623
m_s_a said:He is not at the end a presence
Why ؟
The previous way the others is suitable ? why ?...
Look please:
Now I don't understand what your picture is trying to tell me either. The proof of the limit in your first post is just fine.
- #6
m_s_a
- 88
- 0
Dick said:Now I don't understand what your picture is trying to tell me either. The proof of the limit in your first post is just fine.
I did not understand your intention ?
I do not have a confirmation of the response
But look at the next example:
I apologize
Second : on the axis z = y^2
Attachments
Last edited:
- #7
HallsofIvy
Science Advisor
Homework Helper
- 42,989
- 975
You have now posted 3 different pictures that appear to involve three different problems. As Dick told you before, the first is correct. This third one is also correct- except for spelling: since you get two different limits by approaching (0,0) along two different paths, the limit does not exist.
I'm not sure what the second picture was supposed to represent. But one thing you should be careful about: The line y= 2x, for example, in R2, is not in the complex plane.
I'm not sure what the second picture was supposed to represent. But one thing you should be careful about: The line y= 2x, for example, in R2, is not in the complex plane.
- #8
m_s_a
- 88
- 0
HallsofIvy said:You have now posted 3 different pictures that appear to involve three different problems. As Dick told you before, the first is correct. This third one is also correct- except for spelling: since you get two different limits by approaching (0,0) along two different paths, the limit does not exist.
My answer of the first question :
is correct or a mistake?
I'm not sure what the second picture was supposed to represent. But one thing you should be careful about: The line y= 2x, for example, in R2, is not in the complex plane.
My answer of the first question :
is correct or a mistake?
remember:
x=(z+z')/2
y=(z-z')/2i
z'=z par
Attachments
- #9
Dick
Science Advisor
Homework Helper
- 26,259
- 623
lim(z->0) is not the same as lim(x->0) or lim(y->0). It's lim(x->0 AND y->0).
- #10
m_s_a
- 88
- 0
Dick said:lim(z->0) is not the same as lim(x->0) or lim(y->0). It's lim(x->0 AND y->0).
Look into the proof of Coshi theory - Riman
f'(z)=f'(x)=f'(y)
no f'(z)=f'(x)+f'(y)
- #11
Dick
Science Advisor
Homework Helper
- 26,259
- 623
m_s_a said:Look into the proof of Coshi theory - Riman
f'(z)=f'(x)=f'(y)
no f'(z)=f'(x)+f'(y)
What have derivatives got to do with it? You were posting limit problems. Or something. I give up. I don't know what your question or problem is.
- #12
m_s_a
- 88
- 0
I support the second solution
And I am not sure
And I am not sure
- #13
Dick
Science Advisor
Homework Helper
- 26,259
- 623
If you are asking does |z|^2/z approach 0 as z approaches 0. Then, it does. You're first argument is fine. If you think there is a problem because the limit of z* as z approaches 0 is path dependent, then you are wrong. The limit is 0.
What is the purpose of studying compound functions?
The purpose of studying compound functions is to understand how different functions can be combined to create more complex mathematical relationships. This knowledge can be applied in various fields such as physics, engineering, economics, and computer science.
What are number paths in compound functions?
Number paths in compound functions refer to the sequence of numbers that are used as inputs and outputs in a compound function. These numbers follow a specific pattern and can be visualized as a path on a number line.
Why is it important to remember number paths in compound functions?
Remembering number paths in compound functions is important because it allows us to understand how the inputs and outputs are related and how the function behaves. This knowledge can help us make predictions and solve problems involving compound functions.
What are some common mistakes when working with compound functions?
Some common mistakes when working with compound functions include not following the correct order of operations, misinterpreting the number paths, and using incorrect inputs. It is important to carefully follow the rules and understand the concept behind the function to avoid these mistakes.
How can I improve my understanding of compound functions and number paths?
To improve your understanding of compound functions and number paths, you can practice solving problems, work with different types of functions, and create visual representations such as graphs or number lines. It is also helpful to seek guidance from a teacher or tutor if you are struggling with the concept.
Similar threads
-
Calculus and Beyond Homework Help
- Replies
- 12
- Views
- 783
-
Calculus and Beyond Homework Help
- Replies
- 9
- Views
- 863
-
Calculus and Beyond Homework Help
- Replies
- 4
- Views
- 915
-
Calculus and Beyond Homework Help
- Replies
- 2
- Views
- 856
-
Calculus and Beyond Homework Help
- Replies
- 15
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 27
- Views
- 735
-
Calculus and Beyond Homework Help
- Replies
- 3
- Views
- 284
-
Calculus and Beyond Homework Help
- Replies
- 7
- Views
- 832
-
Calculus and Beyond Homework Help
- Replies
- 2
- Views
- 321
-
Calculus and Beyond Homework Help
- Replies
- 11
- Views
- 928
Share: