- #1
- 1,591
- 3
Though you guys might find this interesting. It's something I've not seen before. Consider the ODE:
[tex]\frac{dy}{dx}=f(x,y)[/tex]
and the attached plot below.
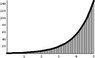
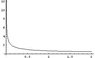
The blue represents the surface for the function f(x,y) (some particular example for the plot) in the first quadrant.
The vertical lines represents the line integral along the curve y(x) that is a (particular) solution for the ODE.
That is, we can say:
[tex]y(x)=y_0+\int_{y(x)} f(u,v) ds[/tex]
And thus solving the differential equation amounts to finding a curve in the x-y plane such that the value of the line integral starting from the point [itex](x_0,y_0)[/itex], along the curve y(x), to the point (x,y(x)), plus [itex]y_0[/itex] is the same as the value of y(x).
Why do I find that amazing?
[tex]\frac{dy}{dx}=f(x,y)[/tex]
and the attached plot below.
The blue represents the surface for the function f(x,y) (some particular example for the plot) in the first quadrant.
The vertical lines represents the line integral along the curve y(x) that is a (particular) solution for the ODE.
That is, we can say:
[tex]y(x)=y_0+\int_{y(x)} f(u,v) ds[/tex]
And thus solving the differential equation amounts to finding a curve in the x-y plane such that the value of the line integral starting from the point [itex](x_0,y_0)[/itex], along the curve y(x), to the point (x,y(x)), plus [itex]y_0[/itex] is the same as the value of y(x).
Why do I find that amazing?
Attachments
Last edited: