- #1
caner_cem
- 8
- 0
[SOLVED] A Problem About Satellite
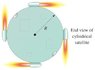
To get a flat, uniform cylindrical satellite spinning at the correct rate, engineers fire four tangential rockets as shown in the figure.
If the satellite has a mass of 3700 kg, a radius of 5.0 m, and the rockets each add a mass of 250 kg, what is the required steady force of each rocket if the satellite is to reach 33 rpm in 5.5 min, starting from rest?
can anyone help me to solve this problem?
Homework Statement
To get a flat, uniform cylindrical satellite spinning at the correct rate, engineers fire four tangential rockets as shown in the figure.
If the satellite has a mass of 3700 kg, a radius of 5.0 m, and the rockets each add a mass of 250 kg, what is the required steady force of each rocket if the satellite is to reach 33 rpm in 5.5 min, starting from rest?
can anyone help me to solve this problem?
Attachments
Last edited: