- #1
sahilmm15
- 100
- 27
In the below picture I understood the problem and also understood the solution. But I am not clear on why did they choose this particular method. So my question is why did they divided 50 with powers of 2 and 3, and what relation does ##50## have with ##50!## ( I am clear on the solution part but I am clueless how would have the author thought of the problem.) Thanks!
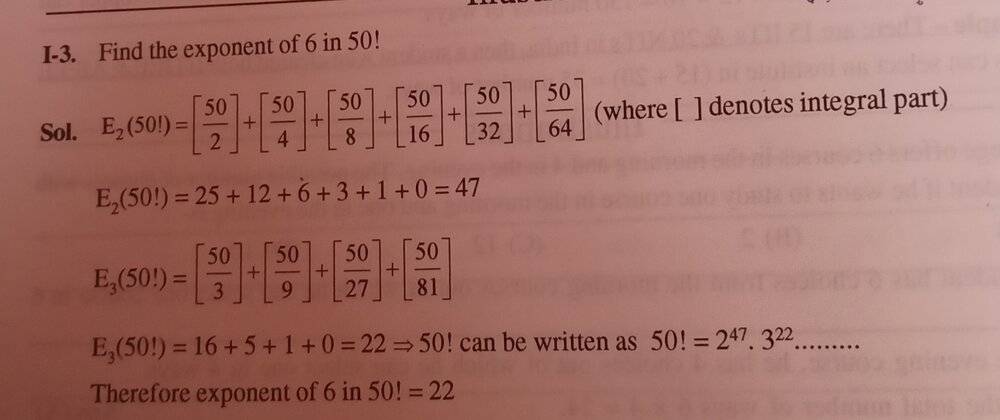
Last edited by a moderator: