- #1
aosome23
- 16
- 0
So, is there anyway to make the dot product change linearly? What I mean by this is when the angle is 45 degrees, I want it to be 0.5 instead of 0.7071 as you can see in this image:
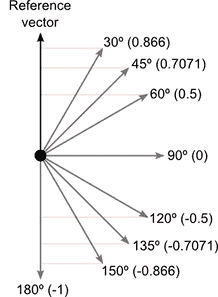
Instead I want 45 degrees to be 0.5, 60 degrees to be 0.33 and 30 degrees to be 0.66. Same would apply for the other side(135 should be -0.5)
Thank you
Instead I want 45 degrees to be 0.5, 60 degrees to be 0.33 and 30 degrees to be 0.66. Same would apply for the other side(135 should be -0.5)
Thank you