- #1
jncarter
- 49
- 0
Homework Statement
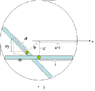
A thin rod of length 2l and linear mass density of [itex]\lambda[/itex] is constrained to move with its ends on a circle of radius a, where a>l. The circle is in the vertical plane (gravity is present). The contacts between the circle and rod are frictionless.
Part A: Write down the Lagrangian describing the motion of the rod.
Part B: Calculate the frequency of oscillation for small departures from equilibrium.
Homework Equations
The Lagrangian: L = [itex]\frac{1}{2}mv^2[/itex] + mgh. Where h is the height and is some function of the angle [itex] \theta.[/itex]
The Euler-Lagrange equation: [itex]\frac{d}{dt}[/itex][itex]\frac{\partial L}{\partial q}[/itex] = [itex]\frac{\partial L}{\partial \dot{q}}[/itex]
The Attempt at a Solution
The distance between the center of mass and the center of the circle (call it L) must remained fixed, the center of mass moves like a simple pendulum. Its Lagrangian is given by
[itex]L = \lambda l L^2\dot{\theta}^2 - 2\lambda gLcos\theta[/itex]
and would have a period of [itex]\sqrt{\frac{L}{g}}[/itex].I can't tell if I have to describe the motion at some point [itex]dl = \sqrt{dx^2 + dy^2} [/itex]from the center of mass (with coordinates [itex]X=Lsin \theta[/itex] [itex]Y =Lcos \theta[/itex]. I think it comes down to a problem with understanding the geometry of the problem. I also can't remember what ends up happening to the Lagrangian of an extended body.
Attached is a picture of the system.Thank you for any help!
Attachments
Last edited: