- #1
JJRKnights
- 53
- 0
I found an answer, but I am skeptical.
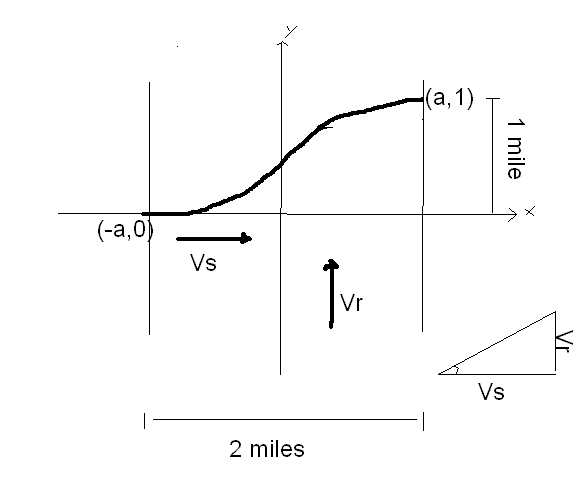
What must the swimmer's speed, vs, be in order that he drifts only 1 mile downstream as he crosses the river?
The width of the river = 2 miles
The velocity of the river, vr = 3(1-x^2)
Relevant equations:
tanα=vr/vs
dy/dx = tanα
vr = v0(1-x^2/a^2)
Image:
So I started off with:
tanα=vr/vs
plugged in dy/dx for tanα, and vr = 3(1-x^2)
dy/dx = (3/vs)(1-x^2)
I assumed that vs was a constant.
∫dy/dx = (3/vs)∫(1-x^2)dx
y = (3/vs)(x - 1/3 x^3) + C
plugged in initial values y(-1) = 0,
0 = (3/vs)((-1) - 1/3(-1)^3) + C
((-1) - 1/3(-1)^3) = -2/3
0 = (3/vs)(-2/3) + C
C = 2/vs
now I have the equation all with 1 unknown:
y = (3/vs)(x - 1/3 x^3) + 2/vs
here is the part where I just improvised not really knowing what to do...
I figured that if I used the initial values, I wouldn't get my vs, so I used the final values:
y(1)=1
1 = (3/vs)(1 - 1/3) + 2/vs
and for this one I get that:
vs = 4 mi/h
What must the swimmer's speed, vs, be in order that he drifts only 1 mile downstream as he crosses the river?
The width of the river = 2 miles
The velocity of the river, vr = 3(1-x^2)
Relevant equations:
tanα=vr/vs
dy/dx = tanα
vr = v0(1-x^2/a^2)
Image:
So I started off with:
tanα=vr/vs
plugged in dy/dx for tanα, and vr = 3(1-x^2)
dy/dx = (3/vs)(1-x^2)
I assumed that vs was a constant.
∫dy/dx = (3/vs)∫(1-x^2)dx
y = (3/vs)(x - 1/3 x^3) + C
plugged in initial values y(-1) = 0,
0 = (3/vs)((-1) - 1/3(-1)^3) + C
((-1) - 1/3(-1)^3) = -2/3
0 = (3/vs)(-2/3) + C
C = 2/vs
now I have the equation all with 1 unknown:
y = (3/vs)(x - 1/3 x^3) + 2/vs
here is the part where I just improvised not really knowing what to do...
I figured that if I used the initial values, I wouldn't get my vs, so I used the final values:
y(1)=1
1 = (3/vs)(1 - 1/3) + 2/vs
and for this one I get that:
vs = 4 mi/h