- #1
Jhenrique
- 685
- 4
Is correct to affirm that:
[tex]| \nabla \times \vec{f} | = \nabla \times \vec{f} \cdot \hat{n}[/tex]?
I asked thinking in this definition:
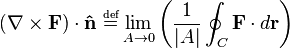
http://en.wikipedia.org/wiki/Curl_(mathematics)
Ie, if the affirmation above is correct, so, is correct to express the definition aboce as:
[tex]\lim_{A \rightarrow 0} \frac{1}{|A|}\oint _{C} \vec{F}\cdot d\vec{r} = |\nabla \times \vec{f} |[/tex]?
[tex]| \nabla \times \vec{f} | = \nabla \times \vec{f} \cdot \hat{n}[/tex]?
I asked thinking in this definition:
http://en.wikipedia.org/wiki/Curl_(mathematics)
Ie, if the affirmation above is correct, so, is correct to express the definition aboce as:
[tex]\lim_{A \rightarrow 0} \frac{1}{|A|}\oint _{C} \vec{F}\cdot d\vec{r} = |\nabla \times \vec{f} |[/tex]?