What are the numerical values of a1 and a2 in this AC transformer circuit?

[chem_is_lovex]

Homework Statement

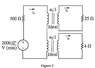
The sinusoidal voltage source in the circuit shown in Fig. 2 is developing an RMS voltage of 2000V. The 4ohm load in the circuit is absorbing 4 times as much average power as the 25ohm load. The two loads are matched to the sinusoidal source that has an internal impedance of 500<0 ohms. (please see attached circuit)
Specify the numerical values of a1 and a2

Homework Equations

(V1/V2)/(N1/N2)=(I1/I2)=a

The Attempt at a Solution

I have no idea on how to do this :( can someone please help me? We haven't done much on questions like this. thanks

Circuit diagram

 

[gneill]

Can you specify the currents in the secondaries in terms of the a's and I1? How about the power being dissipated in the secondary resistors?

 

[chem_is_lovex]

Can you specify the currents in the secondaries in terms of the a's and I1? How about the power being dissipated in the secondary resistors?

ummm... The I2=a1*I1
and I3=a2*I1?

and is the power being dissapated: P=(I2^2)*R2
and P=(I3^2)*R3?

 

[gneill]

ummm... The I2=a1*I1
and I3=a2*I1?

and is the power being dissapated: P=(I2^2)*R2
and P=(I3^2)*R3?

Yes, so what are the powers in terms of I1? Also, you're given a relationship between those powers, so determine the relationship between the a's.

 

[Chrisas]

You now need to find out how to use the givens in the problem statement.

The two loads are matched to the sinusoidal source that has an internal impedance of 500 ohm

From this statement you can compute a number for I_1 and find the voltage across the internal impedance and the voltage across the left coils of the transformers. You need to consider what it means for the loads to be matched to the source. From the answer for I_1, you can find the power being put into the left side of the transformers.

The 4ohm load in the circuit is absorbing 4 times as much average power as the 25ohm load.

Knowing the power input to the transformer and the above statement, you should be able to figure how much power is being spent in each loop on the right. Knowing the powers can you now find I_2 and I_3?

Knowing all the currents allows you finally to find a1 and a2.

 

[chem_is_lovex]

Yes, so what are the powers in terms of I1? Also, you're given a relationship between those powers, so determine the relationship between the a's.

ok, I tried that and I got a ratio of a2=(5*a1)/2

now do I sub this back into one of the power equations? and is this ratio even right?

 

[gneill]

ok, I tried that and I got a ratio of a2=(5*a1)/2

now do I sub this back into one of the power equations? and is this ratio even right?

Can you show your work for finding the ratio of the a's? It's very nearly right...

Once you've determined that relationship between the a's you need to find another so that you will have two equations in two unknowns. This second equation involves the "matched" property of the loads and source impedance. We'll get to that


By the way, you can produce superscripts and subscripts by using the x² and x₂ icons in the reply box header.

 

[chem_is_lovex]

ok, I've attached my working out... as you can tell I'm not very good at simplifying equations, so please bear with me.

 

[gneill]

I think that there's a small problem in your end game

 

[bill_dcx3]

Hi i have the same problem

i am unsure how to find the value of I₁ and how to calculate the power dissipated in the left loop. Do you use V₁*I₁=V₂*I₂? and therefore V₂=sqrt(V₁*I₁*R₂)?

Also i am a bit confused of the current in the left hand loop.

Is I1 = (V₁)/(R₁) meaning I₁= (2000<0)/(500<0) = 4<0 A? Or does the internal resistance of the source come into play meaning that for the left hand loop, I₁ = (2000<0)/(500<0)+(500<0) = 2<0 A *500 ohm resistor + 500 ohms of internal resistance*

Could you please tell me what the Current is in the left hand loop (I₁) and what the transformer voltages are for V₂ & V₃. I think would you then use V₂=sqrt(V₁*I₁*R₂) & V₃=sqrt(V₁*I₁*R₃) to calculate the voltage, but I am not 100% sure.




Note:
I know that it should be in terms of impedance (Z), not resistance (R). For simplicity I am assuming they are the same.

for the previous post
a₂ = 5 a₁, is what i assume your getting at.

 

[gneill]

Rather than go directly for the current in the primary loop, it may be easier to consider the given claim that the loads are matched to the source's impedance. Transformers have the property that impedances in the secondary circuits are 'reflected' back into the primary circuit. So a resistance R in a secondary loop of an N:1 transformer will cause the primary loop to behave as though there was a series resistance N²R in it.

What should be the total resistance reflected into the primary circuit if the loads are matched to the source impedance (given as 500 Ohms)?

 

[bill_dcx3]

Okay, I've taken the reflective advice and matched it with what i already have figured i think I've got it.

Anyway, i get
a₁=2 a₂=10
I₂= 8 A I₃=40 A
I₁= 4 A

For the 25 ohm resisior in circuit 2
P=1600W V=200 V

For the 4 ohm resistor
P=6400W V=160 V

If its not to much of you, could you check to see if i am correct? i would like to be as certain as possible.

 

[chem_is_lovex]

I think that there's a small problem in your end game

ohhhh, yeah. ok, I didn't expand the 2(a_2I1) and I get a₂I₁=5. next I did some working (attached) and I found that a₂=5a₁. What do I do after? I tried to sub it into some equations, but I can't seem to get a decent answer... is the working out I've done anywhere close to right?

 

[bill_dcx3]

Just realized, does the internal impedance of the 2000<0 V have an effect on the left hand circuit? i can't decide if the current I₁ is equal to 2<0 A or 4<0 A. I mention it before when i said

*Is I1 = (V₁)/(R₁) meaning I₁= (2000<0)/(500<0) = 4<0 A? Or does the internal resistance of the source come into play meaning that for the left hand loop, I₁ = (2000<0)/(500<0)+(500<0) = 2<0 A *500 ohm resistor + 500 ohms of internal resistance*

 

[gneill]

The source's internal impedance is in series with the source voltage, and you can't avoid or ignore it. The load impedances (resistances in this case) will be reflected into the primary circuit, too, and those reflected impedances will have to be added. So the primary's current will be
$$I_1 = \frac{2000V}{Internal + Reflected} = \frac{2000V}{500 \Omega + 500 \Omega}$$

 

[bill_dcx3]

Got it now, thanks a lot.

 

[chem_is_lovex]

can someone please answer my question too? thanks, I'm nearly finished this question...

 

[bill_dcx3]

Hope this helps