- #1
Alan Sammarone
- 5
- 1
Hello. I am having some trouble to understand conceptually the behaviour of such a system:
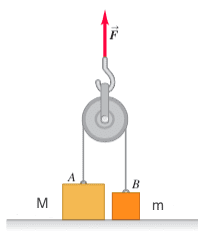
So, both blocks are in contact with the floor, one has mass M and the other has mass m. Then we apply an upwards force F on the axel of the pulley. How does the system behave?
My initial thought is that if
$$ \vec{F} > (m + M)g $$
Then the whole system accelerates upwards. If that's not the case, then only the lighter mass would accelerate (upwards).
That doesn't seem to be case. Particularly, it seems that i should consider that the tension in the string is half the applied force. In general, any pulley attached to a ceiling is going to exert double the tension force on the ceiling. Why is that?So, my question is: how should i go about analysing the behaviour of this system, conceptually, and why? And why is the tension half the force the pulley experiences (if that's even true)?
Thanks!
(This is my first post here. This is not a Homework question, but it was in a book that I've been studying. If I've posted that in the wrong place, i am sorry)
So, both blocks are in contact with the floor, one has mass M and the other has mass m. Then we apply an upwards force F on the axel of the pulley. How does the system behave?
My initial thought is that if
$$ \vec{F} > (m + M)g $$
Then the whole system accelerates upwards. If that's not the case, then only the lighter mass would accelerate (upwards).
That doesn't seem to be case. Particularly, it seems that i should consider that the tension in the string is half the applied force. In general, any pulley attached to a ceiling is going to exert double the tension force on the ceiling. Why is that?So, my question is: how should i go about analysing the behaviour of this system, conceptually, and why? And why is the tension half the force the pulley experiences (if that's even true)?
Thanks!
(This is my first post here. This is not a Homework question, but it was in a book that I've been studying. If I've posted that in the wrong place, i am sorry)
Last edited: