Acceleration of Hinges

[Abhijeet Verma]

This is a problem posted by a member on Brilliant.org (https://brilliant.org/problems/acceleration-of-hinges/). I found one way to solve the problem, but it is really long, and i am looking for some different solutions. The problem is-

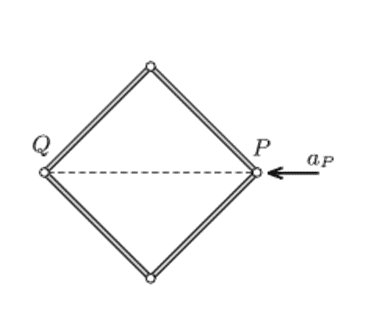Four similar rods of uniform density are connected with frictionless hinges. This frame is placed on a horizontal smooth tabletop, such that its shape is a square. Vertex P is acted upon by a horizontal force in the direction of the diagonal, and due to this force it begins to move at an acceleration of $a_P$.

If the initial acceleration of the opposite vertex Q is $a_Q= k.a_P$ then find k.

k is positive if Q moves away from P and k is negative if Q moves closer to P.

Please post any solution or approach that can be applied in it.
Thanks.

 

[A.T.]

I found one way to solve the problem, but it is really long

Is at least the result you get from the long solution something simple? Then there is a chance for a simpler way to solve it.

 

[Abhijeet Verma]

Is at least the result you get from the long solution something simple? Then there is a chance for a simpler way to solve it.

I solved it using the work-energy theorem, by finding the energy of the system after displacing by a small amount, and the work done by the force applied at point P, somewhat similar to what someone posted there. Finding the energy is pretty long, but yes the results are simple expressions in $a_P$ and $a_Q$.

 

[A.T.]

I solved it using the work-energy theorem, by finding the energy of the system after displacing by a small amount, and the work done by the force applied at point P, somewhat similar to what someone posted there. Finding the energy is pretty long, but yes the results are simple expressions in $a_P$ and $a_Q$.

I would try to use the center of mass frame, where the kinematics is nicely symmetrical. The center of mass frame is non-inertial, but has a known acceleration, and thus a known inertial force field. Since the inertial force field is uniform, it doesn't create any torques at the bars, around their centers of mass.

 

[wrobel]

First you must obtain differential equations of motion not at the single moment but for all $t$. For $t>0$ the square will deform to a rhombus. So this is a system with two degrees of freedom

Let $X$ be the axis of inertial frame and $x$ be the coordinate of the center of the rhombus. The generalized coordinates are $\alpha,x$.

We shall assume that the force $\boldsymbol F$ does not depend on time. It does not matter since we will consider the differential equations at initial moment only. Then find the kinetic energy to this system $T=T(\dot\alpha,\dot x,\alpha,x)$ You will see that actually $T$ does not depend on $x,\alpha$. And write the Lagrange equations
$$\frac{d}{dt}\frac{\partial T}{\partial \dot x}-\frac{\partial T}{\partial x}=Q_x,\quad \frac{d}{dt}\frac{\partial T}{\partial \dot \alpha}-\frac{\partial T}{\partial \alpha}=Q_\alpha.$$
The first equation will be $4m\ddot x=F$ ($m$ is the mass of the rod), but the second one is not so evident, you have to calculate for it.

 

[wrobel]

I usually give this problem to students, once I proposed it here for methodology discussion https://www.physicsforums.com/threads/a-problem-about-the-frame.871175/

 

[Abhijeet Verma]

First you must obtain differential equations of motion not at the single moment but for all $t$. For $t>0$ the square will deform to a rhombus. So this is a system with two degrees of freedom

Let $X$ be the axis of inertial frame and $x$ be the coordinate of the center of the rhombus. The generalized coordinates are $\alpha,x$.

We shall assume that the force $\boldsymbol F$ does not depend on time. It does not matter since we will consider the differential equations at initial moment only. Then find the kinetic energy to this system $T=T(\dot\alpha,\dot x,\alpha,x)$ You will see that actually $T$ does not depend on $x,\alpha$. And write the Lagrange equations
$$\frac{d}{dt}\frac{\partial T}{\partial \dot x}-\frac{\partial T}{\partial x}=Q_x,\quad \frac{d}{dt}\frac{\partial T}{\partial \dot \alpha}-\frac{\partial T}{\partial \alpha}=Q_\alpha.$$
The first equation will be $4m\ddot x=F$ ($m$ is the mass of the rod), but the second one is not so evident, you have to calculate for it.

Sorry, but i don't know Lagrangian Mechanics and hence don't understand the solution.