- #1
Daminc
- 39
- 0
Hi following a link on another thread I began to read On The Electrodynamics Of Moving Bodies
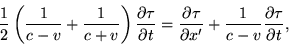
should equal
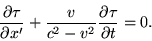
but I end up with a minus instead of a plus between the two fractions(in the last equation).
I've gone through my calculations but I cannot see where I've gone wrong.
I could post my working out if necessary but it might be hard to read in this format
should equal
but I end up with a minus instead of a plus between the two fractions(in the last equation).
I've gone through my calculations but I cannot see where I've gone wrong.
I could post my working out if necessary but it might be hard to read in this format