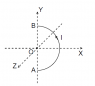- #1
Saitama
- 4,243
- 93
Homework Statement
A conductor carrying current ##I## is in the form of a semicircle AB of radius ##R## and lying in xy-plane with it’s centre at origin as shown in the figure. Find the magnitude of ##\oint \vec{B}\cdot \vec{dl}## for the circle ##3x^2+3z^2=R^2## in the xz plane due to curve AB.
(Ans: ##(2-\sqrt{3})\frac{\mu_0 I}{2}##)
Homework Equations
The Attempt at a Solution
From Ampere's law:
$$\oint \vec{B}\cdot \vec{dl}=\mu_0 I_{enclosed}$$
There is no current passing through the loop ##3x^2+3z^2=R^2##, so for this loop, RHS for ampere's law is zero hence answer should be zero but it isn't.
Any help is appreciated. Thanks!
Attachments
Last edited: