- #1
esmeco
- 144
- 0
Homework Statement
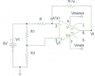
One of the problems question is: Determine the analitical expression that relates the resistive value of the NTC thermistor with the tension Vt.I've come to an expression but I'm not sure if it's correct.Also, the other question of the problem is: Make an analitic description of the circuit.And I'm not sure what they meant to say with "analitical discription of the circuit".
Homework Equations
The Attempt at a Solution
For my first question the expression,which results on the attempt to the solution is: Vt = 5 + R*(-I3) + NTC*(-INTC)
Attachments
Last edited: