- #1
transgalactic
- 1,395
- 0
i added a file with the curve the is being asked to find
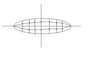
an ellipse is given. its formula is x^2 + 2*y^2=8 .
find the formula of the curve that is being created by the
the centers of the perpendicular lines to the X axes and the ellipse.
i tried to solve this question
by putting the Y^2 on the one side and on the other the rest
and devidind it by 2 .
2y^2=8-x^2
y^2=8-x^2/2
y=V(8-x^2/2)
(v=root simbol)
the curve that in the center always smaller in height by 2
so i devided the formula by 2 to find our curve
y=1/2*V(8-x^2/2)
in my book it gives a different answer
(x^2)/8 +y^2=1
please help
an ellipse is given. its formula is x^2 + 2*y^2=8 .
find the formula of the curve that is being created by the
the centers of the perpendicular lines to the X axes and the ellipse.
i tried to solve this question
by putting the Y^2 on the one side and on the other the rest
and devidind it by 2 .
2y^2=8-x^2
y^2=8-x^2/2
y=V(8-x^2/2)
(v=root simbol)
the curve that in the center always smaller in height by 2
so i devided the formula by 2 to find our curve
y=1/2*V(8-x^2/2)
in my book it gives a different answer
(x^2)/8 +y^2=1
please help