Find the Shortest Route for an Ant in a Cube Shaped Room | Brainteaser

  • Thread starter tanujkush
  • Start date
  • Tags
    Interesting
In summary, the conversation is about a brainteaser involving an ant in a cube shaped room. The ant needs to go from one corner of the floor to the opposite corner on the ceiling, but cannot fly. The shortest route is the body diagonal, but the ant is tired and wants to take the shortest possible route. The solution involves walking diagonally to the corner directly below the desired end point, and then going up for a total walking distance of approximately 2.1415 times the length of the cube.
  • #1
tanujkush
39
0
Ok so here is a brainteaser, you should get it in your second attempt at the max., else consider yourself poor at math :biggrin:

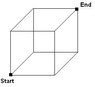
An ant is in one corner of a cube shaped room. (say one of the bottom corners on the floor). The ant decides to go to the opposite corner on the roof, which would fall on the diagonal of the cube. Unfortunately, the ant cannot fly, else it would have taken the body diagonal route of the cube to reach there. But the ant is most tired, and it wants to take the shortest route possible. Help the ant out!
 

Attachments

  • puzzle.JPG
    puzzle.JPG
    3.4 KB · Views: 346
Mathematics news on Phys.org
  • #2
walk diagonally (at 22.5°) along the floor to the middle of the opposite face and then walk diagonally (at 22.5°) up to the opposite corner. A total walking distance of approximately 2.16 times the length of the cube face.
 
  • #3
redargon said:
walk diagonally (at 22.5°) along the floor to the middle of the opposite face and then walk diagonally (at 22.5°) up to the opposite corner. A total walking distance of approximately 2.16 times the length of the cube face.

spot on!
 
  • #4
Have I misunderstood the question? Why not walk diagonally to the corner directly below the End, and then go up. Walking distance is sqrt 2 + 1 times the cube length, approx 2.1415 times the length.
 
  • #5
Gib Z said:
Have I misunderstood the question? Why not walk diagonally to the corner directly below the End, and then go up. Walking distance is sqrt 2 + 1 times the cube length, approx 2.1415 times the length.

walking till the midpoint of the opposite face and then straight to the point end gives you a total distance of sqrt((2a)^2+a^2) = sqrt(5)*a = 2.23606a

walking on the bottom diagonal and then straight up to End is a distance of (sqrt(2)+1)*a = 2.414a>2.3606a
 
  • #6
My bad, something exploded in my brain as I used digits of pi for sqrt 2.
 
  • #7
If the sides of the cube are unfolded to a flat surface, the ant's shortest path will be a straight line
 
  • #8
bpet said:
If the sides of the cube are unfolded to a flat surface, the ant's shortest path will be a straight line

thats exactly the logic! i was asked this question as a part of my mathematics aptitude some time before undergrad, and I was stumped at the time
 

1. What makes a question interesting?

An interesting question is one that sparks curiosity, encourages critical thinking, and leads to meaningful discussions. It can also challenge preconceived notions and push the boundaries of knowledge.

2. How do I come up with an interesting question?

An interesting question can be inspired by everyday observations, current events, personal experiences, or gaps in existing knowledge. It is important to approach the question with an open mind and a willingness to explore various perspectives.

3. Can an interesting question have more than one answer?

Yes, an interesting question can have multiple answers depending on the context, perspective, and evidence presented. This can lead to further discussions and debates, making the question even more engaging.

4. What is the significance of asking interesting questions in scientific research?

Asking interesting questions is crucial in scientific research as it drives the discovery of new knowledge and advancements in various fields. It also allows scientists to challenge existing theories and hypotheses and leads to the development of new ones.

5. Can an interesting question lead to further research?

Absolutely! Interesting questions often lead to new research studies and experiments as scientists strive to find answers and solutions. This continuous cycle of questioning and exploration is essential in advancing our understanding of the world.

Similar threads

What is the shortest path a fly can take in a room with given dimensions?
    • Introductory Physics Homework Help
Replies
4
Views
2K
Finding the Shortest Path for Walking in a Room
    • Introductory Physics Homework Help
Replies
5
Views
4K
What is the Shortest Path for a Fly to Walk Around a Room?
    • Introductory Physics Homework Help
Replies
2
Views
2K
Finding the Shortest Path in a Vector Space
    • Introductory Physics Homework Help
Replies
2
Views
2K
Will the Room Stay Illuminated in Einstein's Photon Box?
    • Optics
Replies
23
Views
5K
WaveGrid - Non-equilibrium Emergence Sandbox
    • Programming and Computer Science
Replies
1
Views
1K
A lot of questions about statics
    • Introductory Physics Homework Help
Replies
15
Views
2K
Mathematica This Week's Finds in Mathematical Physics (Week 262)
    • MATLAB, Maple, Mathematica, LaTeX
Replies
4
Views
2K
Things I Learned from Movies
    • General Discussion
Replies
1
Views
8K
Mathematica This Week's Finds in Mathematical Physics (Week 242)
    • MATLAB, Maple, Mathematica, LaTeX
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top