- #1
xconwing
- 20
- 0
NCEES Reference Handbook p.206Hi,
My question is: In Fig.2, how can R1 and R2 be parallel? If anything, it should be in series because capacitor in the long run is an open.
Thanks ahead.
Last edited:
sophiecentaur said:Hi and welcome.
"Series" and "parallel" are just names. They are not relevant to the analysis of circuits - except for the most elementary cases. But, if you bear in mind that a voltage source (v1) has zero impedance and if you replace it with a piece of wire, then, from the point of view of the C, they are in parallel and the equivalent resistance can be calculated with that formula.
Let i1 be current through R1, ic current through C, and i2 current through R2.xconwing said:how did they come to the equation H(s)?
I tried to do the circuit analysis but it didn't come out the same, will put it up here when i find a decent equation editor
zoki85 said:Let i1 be current through R1, ic current through C, and i2 current through R2.
For sine wave voltage input it holds:
eq.1 i1 = ic+ i2
eq.2 v1 = i1·R1 + ic/(jωC)
eq.3 0 = i2·R2 - ic/(jωC)
From this you find (express) i2.
eq.4 Then, H(s)=H(jω)=v2/v1= (i2·R2)/v1.
eq.5 Finally, when you introduce Rp=R1·R2/(R1+R2), you'll get the result.
zoki85 said:Nothing is missing. 2nd eq. is for the first closed loop: v1 - R1 - C and 3rd eq. is for second closed loop: C-R2.
Do you understand this?
Eqn 3 comes from saying "because C and R2 are connected in parallel, then the voltage across C equals the voltage across R2."xconwing said:Okay, I understand eq.1-3, 2&3 are from KVL. i2 should express from which eq.? Why v1 become a short?
That is how they get the RP to be R1 and R2 parallel right?zoki85 said:i2 to be expressed as one of the solutions to the given system of 3 linear equations (other two solutions are i1 and ic but you don't need them). What "v1 become a short"? I don't understand you
NascentOxygen said:H(s) tells you Vout/Vin. I'm wondering why you are needing to find I2 ?
For a complex impedance, you should be using Zx not Rx. Rx should be used only where the element is known to be a pure resistance.
Oho, looks like you know how to use a voltage divider principle in complex impedance domain:)xconwing said:That is how they get the RP to be R1 and R2 parallel right?
As for finding H(s), the path using system of equation is kind of tedious. My i2 came out to be pretty ugly, maybe the algebra is wrong somewhere or it just simply ugly. I try to use the voltage divider approach, where Rx is C and R2 parrallel.
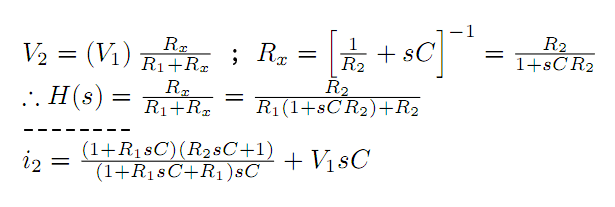
He doesn't need to, but when someone asks questions wether R1 and R2 are in series or parallel it is more pedagogical to show approach with fundamentals of circuit analysis.NascentOxygen said:H(s) tells you Vout/Vin. I'm wondering why you are needing to find I2 ?
Not 100% sure, but my guess is they prefer approach to the problem by the method of Thevenin's theoremxconwing said:Okay, so far the algebra checked off their final equation against my. Though I still don't understand how they see R1 and R2 as being parallel, the v1 is in the way. If you say, turn v1 into a short, why?
Are you drunk?xconwing said:That omega, the way they set it up seem like RP will ALWAYs be equal to capacitor impedance. Is that the case?
R1 and R2 are passive electronic components that are used in Fig.2 to create a voltage divider circuit. This circuit is used to divide the input voltage into two different levels, which can then be used to adjust the gain of the filter circuit.
The values of R1 and R2 can greatly affect the overall performance of the analog filter circuit. These resistors control the gain of the circuit, as well as the frequency response and bandwidth. Choosing the appropriate values for R1 and R2 is crucial in creating an effective filter circuit.
Yes, R1 and R2 can be replaced with other types of resistors, such as variable resistors or trimmer resistors. These types of resistors allow for the adjustment of the gain and frequency response of the filter circuit, making it more versatile for different applications.
Yes, there are limitations to the values of R1 and R2 in Fig.2. These resistors should not be too large or too small, as this can affect the performance and stability of the filter circuit. It is important to choose values that are within the recommended range for the specific circuit being designed.
The values of R1 and R2 can be calculated using the voltage divider equation, Vout = Vin * (R2 / (R1 + R2)). This equation can be rearranged to solve for R1 or R2, depending on the desired gain and input/output voltages. It is also recommended to use a circuit simulator or consult a reference book for specific guidelines and examples on choosing appropriate values for R1 and R2.