Analsis magnet, loretz force

[malawi_glenn]

Homework Statement

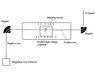
I have a source producing ions of He: He2+ and He+, they are accelerated towards a tandem accelerator, se atteched figure. They are accelerated with a voltage towards the first magnet, were a selection of the ions are made. We only want the He2+ ions the proceed to the tandem accelerator.

Show how this is done in the first analysis magnet.

answer according to my teacher:
the He2+ will get higher energy and therefore less bent, larger radius, then the He+ ions.

Homework Equations

and

The Attempt at a Solution

But according to this, I found that is the opposite, becase F= qvB and the bigger charge, the more force, and hence smaller radius.

$$|F| = qvB \Rightarrow r = \frac{mv}{qB}$$

m and B is the (practically) same for all, I have He+ and He2+ ions. T is kinetical energy.

$$|F| = qvB \Rightarrow r = \frac{mv}{qB}$$$$r\propto \frac{v}{q}$$$$U=T=qV = mc^{2} \Rightarrow v=c\sqrt{1-\left( \frac{mc^{2}}{qV+mc^{2}}\right) ^{2}}}$$Ratio for radius of He2+ and He+ "r(2q)/r(q)"

gives me that He2+ has smaller radius than He+ if they are accelerated with the same potential V and is bent i same magnetiv field.

Non-relativistic gives me:

$$r\propto \frac{v}{q}$$ $$v=\sqrt{\frac{2qV}{m}}$$ $$r\propto \frac{\sqrt{\frac{2qV}{m}}}{q} = \frac{constant}{\sqrt{q}}$$

LOL help =)

 

[malawi_glenn]

And yeah, this last also show that the higher q, the smaller r, and the ion is more bent.

And the attachemt is here too.

 

[malawi_glenn]

lol

should be:

$$|F| = qvB \Rightarrow r = \frac{mv}{qB} r\propto \frac{v}{q} \\ U=T=qV = mc^{2}(\gamma -1) \Rightarrow v=c\sqrt{1-\left( \frac{mc^{2}}{qV+mc^{2}}\right) ^{2}}}$$