- #1
klm
- 165
- 0
A 5.0 kg, 60-cm-diameter disk rotates on an axle passing through one edge. The axle is parallel to the floor. The cylinder is held with the center of mass at the same height as the axle, then released.
What is the cylinder's initial angular acceleration?
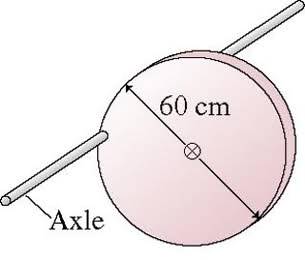
ok so this is what i think i should do:
Torque= I [tex]\alpha[/tex]
and i need to find the F(weight)= mg = (5)(9.8) = 49 N
radius = .5(.6)= .3
Torque= Fd = 49(.3) = 14.7
14.7 = I [tex]\alpha[/tex]
this is the part which i am not sure on, does I = .5 m r^2 = .5(5)(.3^2) = .225
14.7 .225 [tex]\alpha[/tex]
[tex]\alpha[/tex] = 65.33
but this answer is incorrect, and i do not know where i am making the mistake.
What is the cylinder's initial angular acceleration?
ok so this is what i think i should do:
Torque= I [tex]\alpha[/tex]
and i need to find the F(weight)= mg = (5)(9.8) = 49 N
radius = .5(.6)= .3
Torque= Fd = 49(.3) = 14.7
14.7 = I [tex]\alpha[/tex]
this is the part which i am not sure on, does I = .5 m r^2 = .5(5)(.3^2) = .225
14.7 .225 [tex]\alpha[/tex]
[tex]\alpha[/tex] = 65.33
but this answer is incorrect, and i do not know where i am making the mistake.