- #1
stunner5000pt
- 1,461
- 2
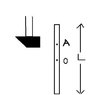
A homogenous rod of length L and mass M is initially at rest on a horizontal frictionless table in teh lab.
The rod is then hit with a hammer, at a point A which is at a distance d from teh center point of the rod. The blow is in the direction perpendicular to the rod. The blow transfers momentum P to the rod. It is assumed that the duration of hte blow is so short taht we can neglect the motion of the rod during the blow. The known quantities are L, M, d, and P
1. Determine the velocity of the center of mass of the rod after the blow.
Now it DOESNt say that the point O is a fixed point so the rod is going to be kicked off in some direction with translational motion too.
relative to the rod the hammer has angular momentum L = dp
if you conserve angular momentum
[tex] d p = \frac{1}{12} ML^2 \omega + Mv[/tex]
well this FAR from what the book says
the book says the velocity = P/ M
but this is assuming that the whole [itex] I \omega [/itex] term is one?! how!?
2.Determine the kinetic energy of the rod after the blow
[tex] \frac{1}{2} m_{hammer} v^2 = \frac{1}{2} I \omega^2 + \frac{1}{2} mv^2 [/tex]
[tex] \frac{1}{2} Pv = \frac{1}{2} \frac{1}{12} ML^2 \omega^2 + T [/tex]
what we need to find is T anyway that's why
[tex] T = \frac{P^2}{2M} - \frac{1}{2} \frac{1}{12} ML^2 \omega^2 [/tex]
but [tex] \omega = \frac{v}{r} = \frac{P}{Mr}[/tex] soo
[tex] T = \frac{P^2}{2M} - \frac{1}{2} \frac{1}{12} ML^2 \frac{P^2}{M^2 r^2} [/tex]
[tex] T = \frac{P^2}{2M} - \frac{P^2}{2M} \frac{L^2 d}{12} [/tex]
did i go wrong somehere here??
Assume there is a poin t C on the rod which - just after the blow - is at rest relative to the table
3. Determine the distance OC. Under what conditions is C a point on the rod??
leave this for later
The rod is then hit with a hammer, at a point A which is at a distance d from teh center point of the rod. The blow is in the direction perpendicular to the rod. The blow transfers momentum P to the rod. It is assumed that the duration of hte blow is so short taht we can neglect the motion of the rod during the blow. The known quantities are L, M, d, and P
1. Determine the velocity of the center of mass of the rod after the blow.
Now it DOESNt say that the point O is a fixed point so the rod is going to be kicked off in some direction with translational motion too.
relative to the rod the hammer has angular momentum L = dp
if you conserve angular momentum
[tex] d p = \frac{1}{12} ML^2 \omega + Mv[/tex]
well this FAR from what the book says
the book says the velocity = P/ M
but this is assuming that the whole [itex] I \omega [/itex] term is one?! how!?
2.Determine the kinetic energy of the rod after the blow
[tex] \frac{1}{2} m_{hammer} v^2 = \frac{1}{2} I \omega^2 + \frac{1}{2} mv^2 [/tex]
[tex] \frac{1}{2} Pv = \frac{1}{2} \frac{1}{12} ML^2 \omega^2 + T [/tex]
what we need to find is T anyway that's why
[tex] T = \frac{P^2}{2M} - \frac{1}{2} \frac{1}{12} ML^2 \omega^2 [/tex]
but [tex] \omega = \frac{v}{r} = \frac{P}{Mr}[/tex] soo
[tex] T = \frac{P^2}{2M} - \frac{1}{2} \frac{1}{12} ML^2 \frac{P^2}{M^2 r^2} [/tex]
[tex] T = \frac{P^2}{2M} - \frac{P^2}{2M} \frac{L^2 d}{12} [/tex]
did i go wrong somehere here??
Assume there is a poin t C on the rod which - just after the blow - is at rest relative to the table
3. Determine the distance OC. Under what conditions is C a point on the rod??
leave this for later
Attachments
Last edited: