- #1
Fascheue
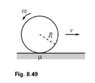
I’m not quite sure where to put this post so forgive me if it’s misplaced, but can somebody explain why the angular velocity in the picture here appears to be in the opposite direction as I would expect if the velocity is in the direction that is is.
I’m not looking to solve this problem (that’s why I didn’t post this in the homework thread), I’m just wondering why the angular velocity is counter-clockwise and the velocity is to the right.
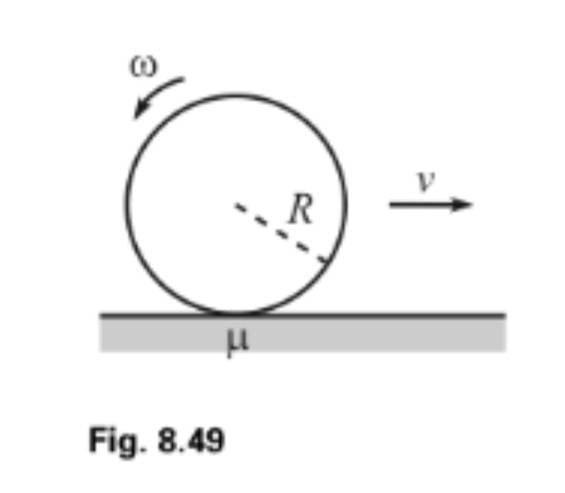

I’m not looking to solve this problem (that’s why I didn’t post this in the homework thread), I’m just wondering why the angular velocity is counter-clockwise and the velocity is to the right.