Rotate Area Bounded by y=5, y=x+(4/x) about x=-1: Verify Limits of Int.

[tony873004]

Rotate the area bounded by
$$y = 5,\,y = x + (4/x)$$
about x=-1

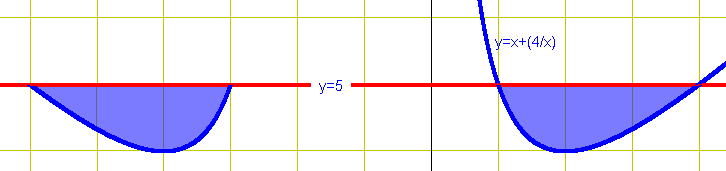
Verify the limits of integration
$$x + \left( {4/x} \right) = 5,\,\,x = 1\& 4$$

solve
$$\begin{array}{l} \int\limits_1^4 {2\pi r\,h\,dx} \\ h = 5 - \left( {x + \left( {4/x} \right)} \right),\,\,r = x + 1 \\ 2\pi \int\limits_1^4 {\left( {x + 1} \right)\left( {5 - \left( {x + \left( {4/x} \right)} \right)} \right)} \,dx \\ \\ 2\pi \int\limits_1^4 {\left( {x + 1} \right)\left( {5 - x - 4x^{ - 1} } \right)} \,dx \\ \\ 2\pi \int\limits_1^4 {\left( {5x - x^2 - 4 + 5 - x - 4x^{ - 1} } \right)} \,dx \\ \\ 2\pi \int\limits_1^4 {\left( {4x - x^2 + 1 - 4x^{ - 1} } \right)} \,dx \\ \\ \end{array}$$
$$\begin{array}{l} 2\pi \int\limits_1^4 {\left( {4x - x^2 + 1 - 4x^{ - 1} } \right)} \,dx \\ \\ 2\pi \left( {\frac{{4x^2 }}{2} - \frac{{x^3 }}{3} + \frac{x}{1} - \frac{{4\ln x}}{1}} \right)_1^4 \\ \\ 2\pi \left( {\frac{{2x^2 }}{1} - \frac{{x^3 }}{3} + \frac{x}{1} - \frac{{4\ln x}}{1}} \right)_1^4 \\ \\ 2\pi \left( {\frac{{6x^2 }}{3} - \frac{{3x^3 }}{3} + \frac{{3x}}{3} - \frac{{12\ln x}}{3}} \right)_1^4 \\ \\ 2\pi \left( {\left( {\frac{{6\left( 4 \right)^2 }}{3} - \frac{{3\left( 4 \right)^3 }}{3} + \frac{{3\left( 4 \right)}}{3} - \frac{{12\ln \left( 4 \right)}}{3}} \right) - \left( {\frac{{6\left( 1 \right)^2 }}{3} - \frac{{3\left( 1 \right)^3 }}{3} + \frac{{3\left( 1 \right)}}{3} - \frac{{12\ln \left( 1 \right)}}{3}} \right)} \right) \\ \\ 2\pi \left( {\left( {\frac{{96}}{3} - \frac{{192}}{3} + \frac{{12}}{3} - \frac{{12\ln \left( 4 \right)}}{3}} \right) - \left( {\frac{6}{3} - \frac{3}{3} + \frac{3}{3} - \frac{0}{3}} \right)} \right) \\ \\ 2\pi \left( {\frac{{96}}{3} - \frac{{192}}{3} + \frac{{12}}{3} - \frac{{12\ln \left( 4 \right)}}{3} - \frac{6}{3}} \right) = \\ \\ 2\pi \left( {\frac{{90}}{3} - \frac{{12\ln 4}}{3}} \right) = 2\pi \left( { - 30 - 4\ln 4} \right) = - 4\pi \left( {15 - 2\ln 4} \right) \\ \\ {\rm{Book says: }}8\pi \left( {3 - \ln 4} \right) \\ \end{array}$$

$${\rm{Book says: }}8\pi \left( {3 - \ln 4} \right)$$
Obviously it can't be negative, but I don't know where I messed up.

 

[tony873004]

I edited the above post to reflect my latest attempt. It's still wrong, so any help would be appreciated.