Area Sector of Hyperbola: Arcsinh & Arcosh Explained w/ Example

[morrobay]

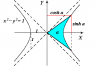
Could someone explain with a numerical example showing how the inverse hyperbolic
functions, arcsinh and arcosh in log form ,can compute the area sector of a unit hyperbola
x^2-y^2=1
If possible with a graph, thanks

 

[benorin]

This picture's worth a thousand area calculations of a sector...

 

[morrobay]

This picture's worth a thousand area calculations of a sector...

Hello that picture from wikipedia is on the hyperbolic functions, sinhx =e^x-e^-x/2
coshx=e^x+e^-x/2
If you substitute a = area for x in the equations above then you can obtain the points on the hyperbola with the sinh(a) as the y cooridinate and cosh(a) as the x cooridinate.
As the ray in picture, that passes through the point cosh(a),sinh(a), sweeps down you can see how the values of area, sinhx,coshx change.
My question is on the inverse hyperbolic functions , arcsinhx= ln(x+sqrt(x^2+1)
See Wikipedia for definitions. Then from the first two lines of that page ,wiki inv hyp func.
continue to 'area sector of unit hyperbola'
Now this is where my question is: what values of x would be used for arcsinh x and arccosh x
to obtain that area sector

 

[benorin]

Reference http://kr.cs.ait.ac.th/~radok/math/mat6/calc31.htm" under the section headed "3.8.4 Further Analogies".