- #1
etf
- 179
- 2
Here is my task and attempt for solution:
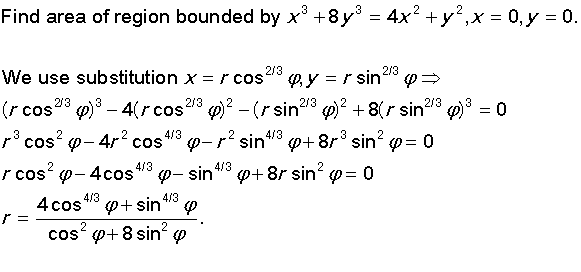
As you can see, I tried with substitutions but I have no idea what to do next.
Any suggestion?
As you can see, I tried with substitutions but I have no idea what to do next.
Any suggestion?
Last edited: