How Do Asymmetrical Stepladder Masses Affect Vertical Forces?

[Swagger]

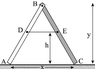
A ladder consists of two legs, AB and BC, that are pinned at joint B and held together by a massless wire between D and E. The two legs are uniform and have the same length (so the ladder forms an isosceles triangle), but the legs have unequal masses. The heavier of the two legs, BC, has a mass of 34.7 kg and is shown shaded gray. The other leg, AB, has a mass of 21.5 kg. The ladder is standing on a smooth floor. The dimensions of the ladder are shown below.

The top of the ladder B is y = 2.45 m above the floor, the distance AC (the base of the ladder) is x = 1.49 m, and the cross brace DE is h = 1.35 m above the floor.

What are the vertical forces on the two legs? (Use "+" if the force component is up, "-" if it is down.) (Ay and Cy)

I know that all of the "internal" forces and torques cancel out if you look at the ladder as a single rigid body. You can then treat it as "center of gravity" problem where two masses are supported on a massless board of length 1.49 m. But I am not sure how to solve it like this? Please Help. Thanks.

 

[Doc Al]

Since the ladder is in equilibrium, you know that (1) the sum of the forces in any direction must be zero, and (2) the sum of the torques about any point must be zero. Since each leg is uniform, you can treat its weight as acting at its center. What's a good point to pick as your axis for finding torques?

Give it a shot.

 

[kyle8921]

I would approach this problem by first drawing a free body diagram of the ladder, showing all the forces acting on it. The forces acting on the ladder are its weight, the normal force from the floor, and the tension in the wire connecting the two legs.

Since the ladder is in equilibrium, the sum of the forces in the vertical direction must be equal to zero. This means that the normal force from the floor must be equal and opposite to the weight of the ladder.

To find the vertical forces on the two legs, we can use the principle of moments. This principle states that the sum of the clockwise moments must be equal to the sum of the counterclockwise moments. In this case, we can take the pivot point to be at joint B, and the moments due to the weight and normal force will cancel out since they act at the same distance from the pivot.

Therefore, the only moment that remains is the moment due to the tension in the wire. Using the equation for moments, we can solve for the vertical forces on the two legs:

(Ay)(1.35m) = (34.7kg)(9.8m/s^2)(1.49m) - (21.5kg)(9.8m/s^2)(2.45m)

Solving for Ay, we get Ay = 170.9 N. Since the normal force is equal and opposite to the weight of the ladder, we can also find Cy by using the equation for the sum of forces in the vertical direction:

Ay + Cy = (34.7kg)(9.8m/s^2) + (21.5kg)(9.8m/s^2)

Therefore, Cy = 480.6 N.

In summary, the vertical forces on the two legs of the ladder are Ay = 170.9 N and Cy = 480.6 N.