- #1
a_hargy
- 16
- 0
Homework Statement
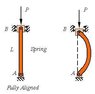
I am trying to determine the deformation of a beam loaded as shown in the attached picture.
where:
P=30kN
L=1m
A=0.000225m^2
E=2.22*10^5MPa
v=0.31
I=4.21875*10^9m^4
Homework Equations
Pcr=pi^2*EI/L
=9.2435kN
where Pcr is the critical load
The Attempt at a Solution
I assume that the deformation of the beam in the vertical direction is not simpily PL/AE as P>Pcr?
I was thinking I could calculate the horizontal deflection of the beam as it buckles and use trig to find the vertical deformation but I cannot find a way to calculate this maximum horizontal deflection. Any ideas?
Thanks in advance.
Adam