- #1
chaoseverlasting
- 1,050
- 3
If someone could tell me how to go about it, I'd really appreciate it. Just point me in the right direction please. Kinda stuck.
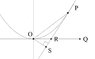
The vertex of a parabola is (-3,1) and it touches the x-axis at the origin. Find the equation of the axis of the parabola.
The vertex of a parabola is (-3,1) and it touches the x-axis at the origin. Find the equation of the axis of the parabola.