- #1
Reverend Shabazz
- 19
- 1
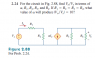
Homework Statement
This problem is Problem 2.24 from Fundamentals of Electric Circuits (5th edition).
The problem is as follows:
Homework Equations
KVL, KCL
The Attempt at a Solution
In the official solution, they assume that the total current in the lefthand loop is ##I_o##, whereas the total current in the righthand loop is ##αI_o##. So they say the current flowing through ##R_4## is ##αI_o##. However, if that is true, then at the node that I circled in red wouldn't KCL be violated: ##I_o + αI_o \neq 0## (unless ##α##=-1)?