- #1
bensthebest
- 3
- 0
Hey I am very new here (litrally signed up 10 mins ago after trying to search the net for this problem)
heres what it looks like in my c/w
i attempted to use ohms law but that would of been pointless. then i looked at the question again and it tells me it has 12v any way but i doubt they would have a question giving me the answer like that and then offer 2 marks for it.
The next question I am stuck on is
again i really have no idea how to work that out.
heres what it looks like in my c/w
so far I've worked out the total resistance of the open circuit but the next question is askingA Battery with an open voltage of 12v and an internal resistance of 0.25[tex]\Omega[/tex] is connected to the circuit terminals A and B shown below (A is the top terminal and B is the bottom i forgot to add it when i copied the picture with paint!)
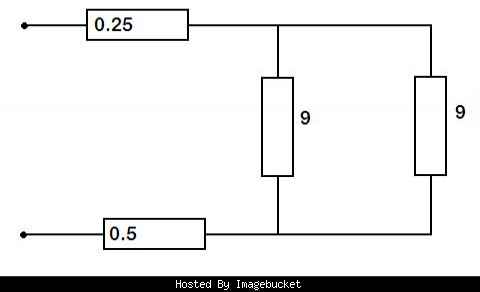
c) the terminal voltage of the battery when it is connected to the circuit
i attempted to use ohms law but that would of been pointless. then i looked at the question again and it tells me it has 12v any way but i doubt they would have a question giving me the answer like that and then offer 2 marks for it.
The next question I am stuck on is
f) The total power dissipated by the battery
again i really have no idea how to work that out.