- #1
Karol
- 1,380
- 22
Homework Statement
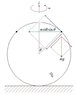
A vertical hoop of mass M can rotate round the z axis without friction. 2 beads of mass m each are at the top and start sliding, one on each side. the hoop starts to rotate with angular velocity ω0. the coefficient of friction is μk=μs=μ and R is the hoop's radius.
What's ω when the beads are at angle θ. Hint: think which parameters are conserved.
Homework Equations
Centripetal force: ##F=m\frac{v^2}{R}=m\omega^2 R##
Angular momentum: ##L=m\omega R^2##
Moment of inertia of a hoop about it's diameter: ##I=\frac{1}{2}MR^2##
The Attempt at a Solution
The angular momentum is conserved since there is no torque round ##\hat{z}##, but i guess the initial angular momentum is 0 since the beads are at the top.
The angular momentum at angle θ: ##L=2m\omega R^2\sin^2\theta##
Attachments
Last edited: