- #1
tlangdon12
- 1
- 0
Hello all
I have a beam bending problem I need some help on.
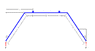
I need to calcuate the deflections at the load (and in the plane of the load) for a simply supported beam with equal point loads overhanging the supports. However my beam is cranked as shown in the attached diagram of the problem geometry.
I know that for a straight beam the formula for the deflection (y) at the loads is
y = Fc2(2c +3b) / 6 EI
where
F = the force applied at each overhang
c = the distance of the overhang
b = the distance between the support
E = the modulus of elasticity of the beam
I = the second area of moment of the beam
(A diagram of the straight beam case is also attached).
Can anyone help me get started on solving this problem?
Thanks
Tony
I have a beam bending problem I need some help on.
I need to calcuate the deflections at the load (and in the plane of the load) for a simply supported beam with equal point loads overhanging the supports. However my beam is cranked as shown in the attached diagram of the problem geometry.
I know that for a straight beam the formula for the deflection (y) at the loads is
y = Fc2(2c +3b) / 6 EI
where
F = the force applied at each overhang
c = the distance of the overhang
b = the distance between the support
E = the modulus of elasticity of the beam
I = the second area of moment of the beam
(A diagram of the straight beam case is also attached).
Can anyone help me get started on solving this problem?
Thanks
Tony