- #1
chetzread
- 801
- 1
Homework Statement
determine deflection of beam
Homework Equations
The Attempt at a Solution
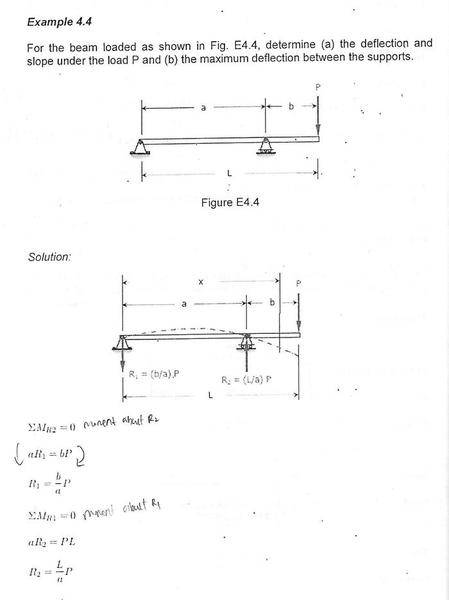
at x=0, y=0 , i found that C2 = LP(a^2)/6 (circled part) but the author gt 0, which is correct?
chetzread said:Homework Statement
determine deflection of beam

Homework Equations
The Attempt at a Solution
at x=0, y=0 , i found that C2 = LP(a^2)/6 (circled part) but the author gt 0, which is correct?
why <x-a> = 0 ?SteamKing said:The author is correct.
##EIy = -\frac{b}{6a}Px^3 + \frac{L}{6a}P<x-a>^3+C_1x+C_2##
When x = 0, y = 0, and the expression <x-a> = 0, due to the definition of the singularity function <x-a>, and C2 = 0 as described in the text.
The way a singularity function is defined:chetzread said:why <x-a> = 0 ?
my notes doesn't hv explanation on thisSteamKing said:The way a singularity function is defined:
<x-a> = 0, if x - a < 0
<x-a> = 1, if x - a > 0
Some other properties are found in this article:
https://en.wikipedia.org/wiki/Singularity_function
You should check your text for the precise definition.
since x - a > 0, so <x-a> = 1 , am i right ? why the author take <x-a> = 0 ?SteamKing said:The way a singularity function is defined:
<x-a> = 0, if x - a < 0
<x-a> = 1, if x - a > 0
Some other properties are found in this article:
https://en.wikipedia.org/wiki/Singularity_function
You should check your text for the precise definition.
When x = 0, <0 - a> = -a; -a < 0; <0-a> = 0, according to the definition of the singularity functionchetzread said:since x - a > 0, so <x-a> = 1 , am i right ? why the author take <x-a> = 0 ?
What about your textbook? Do you have a textbook for this course? What does it say?chetzread said:my notes doesn't hv explanation on this
ok , i have another part of question here . in the working , the maximum deflection occur at x= (1/sqrt rt 3) ,SteamKing said:What about your textbook? Do you have a textbook for this course? What does it say?
chetzread said:ok , i have another part of question here . in the working , the maximum deflection occur at x= (1/sqrt rt 3) ,
why the author ignore the LP[(x-a)^3]/ (6a) at x = (1/sqrt rt 3) ?
by ignoring the at LP[(x-a)^3]/ (6a) at x= (1/sqrt rt 3) , the author assume x-a <0 ?
but , the value of a is unknown , how to know that x-a<0 ?

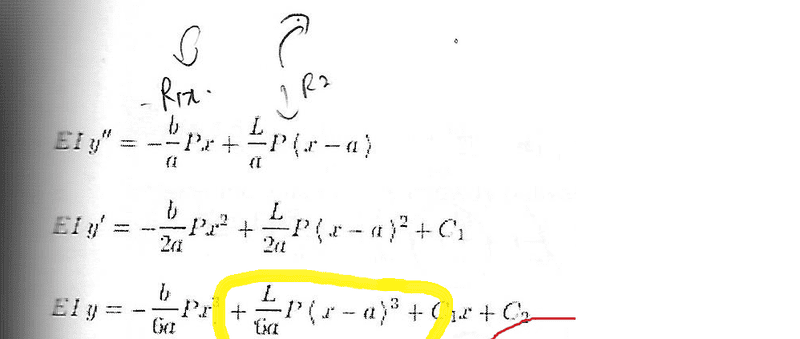
how could that be ? the value of a is unknownSteamKing said:I think the author is clumsily trying to say that the singularity function <x-a> = 0 where the deflection is at a maximum. Instead of saying "do not exist", it would probably be better to say that "<x-a> vanishes" at that location.
Anyhow, once that fact is recognized, then the location x of the maximum deflection can be solved for as illustrated.
No, it isn't. a is the distance between R1 and R2. Look at the beam diagram.chetzread said:how could that be ? the value of a is unknown
if it' so , x > a , so x-a > 0 , so <x-a> should be =1 , right ?SteamKing said:No, it isn't. a is the distance between R1 and R2. Look at the beam diagram.
It's not a which is unknown, it is the value of x at which the deflection is a maximum.chetzread said:if it' so , x > a , so x-a > 0 , so <x-a> should be =1 , right ?
why <x-a> = 0 when deflection is at a maximum ??SteamKing said:I think the author is clumsily trying to say that the singularity function <x-a> = 0 where the deflection is at a maximum. Instead of saying "do not exist", it would probably be better to say that "<x-a> vanishes" at that location.
Anyhow, once that fact is recognized, then the location x of the maximum deflection can be solved for as illustrated.
Specifically, the problem is looking for the location of the maximum deflection between the supports.chetzread said:why <x-a> = 0 when deflection is at a maximum ??
x is located between supports ? but , in the diagram , x span from R1 and beyond R2 ?SteamKing said:Specifically, the problem is looking for the location of the maximum deflection between the supports.
The quantity <x-a> is going to be zero because x is located between between the supports and x = a is the location of the right support. That's just the definition of the singularity function in this case. It helps to check the beam diagram for this problem.
x is the length coordinate of the beam with origin at the left support, i.e. x = 0 there.chetzread said:x is located between supports ? but , in the diagram , x span from R1 and beyond R2 ?
What do you mean ?
Can you explain what is the purpose of having singularity function in beam problem?SteamKing said:x is the length coordinate of the beam with origin at the left support, i.e. x = 0 there.
Sure, x can be used to locate stuff along the entire length of the beam (even beyond the location of the right support), but this particular question asks the student to find the location of maximum deflection between the supports, i.e. find max. δ(x) such that 0 ≤ x ≤ a. Again, refer to the diagram.
Their use can simplify the deflection calculations, especially when the double integration method is used to calculate deflections.chetzread said:Can you explain what is the purpose of having singularity function in beam problem?
if they are not used,then the calculation will become complicated?SteamKing said:Their use can simplify the deflection calculations, especially when the double integration method is used to calculate deflections.
chetzread said:if they are not used,then the calculation will become complicated?
Because that is how the singularity function is defined.I'm still blurred. Taking the case from post#1 as an example, why singularity function said that <x-a> =0 if x<a ?
what do you mean bySteamKing said:Yes. The beam must be split into many different pieces, depending on how it is loaded.
Because that is how the singularity function is defined.
If x < a, then the singularity function <x-a> = 0
If x > a, then the singularity function <x-a> = (x - a)
Just that. If you have many different loads, then the shear force curve and the bending moment curve will be affected by all these different loads and their location along the beam. If you have a single distributed load running the entire length of the beam, that is the simplest loading to analyze. If you have a mix of point loads and distributed loads, or just several point loads, the analysis becomes more complicated. It's hard to describe without having an example problem to use as an illustration.chetzread said:what do you mean by
The beam must be split into many different pieces ?
can you explain using the example in post #1?SteamKing said:Just that. If you have many different loads, then the shear force curve and the bending moment curve will be affected by all these different loads and their location along the beam. If you have a single distributed load running the entire length of the beam, that is the simplest loading to analyze. If you have a mix of point loads and distributed loads, or just several point loads, the analysis becomes more complicated. It's hard to describe without having an example problem to use as an illustration.
Beam deflection is the amount of deformation or bending that a beam experiences when a load is applied to it. It is important because it helps engineers and designers determine the structural integrity and stability of a beam, and allows them to make necessary adjustments to ensure the beam can withstand the desired load without failing.
Beam deflection can be calculated using the Euler-Bernoulli Beam Theory, which takes into account the beam's material properties, geometry, and applied load. The equation for beam deflection can vary depending on the type of load and support conditions, but it typically involves solving for the unknown deflection at a given point using known values of the beam's properties and applied load.
The three main types of loads that can cause beam deflection are point loads, distributed loads, and moment loads. Point loads are concentrated at a specific point on the beam, distributed loads are spread out over a certain length of the beam, and moment loads cause twisting or rotation of the beam at a specific point.
The support conditions of a beam, such as fixed, pinned, or simply supported, can greatly influence the amount of deflection the beam experiences. Different support conditions will result in different equations for calculating beam deflection, and can also affect the distribution of forces and moments along the beam.
Some common methods for solving for unknowns at a given point in beam deflection include using the Macaulay's method, the moment-area method, and the energy method. These methods involve using calculus and/or energy principles to solve for the unknown deflection at a specific point on the beam. Computer software programs and spreadsheets can also be used for more complex beam deflection problems.