- #1
brianinbwangju
- 10
- 0
Homework Statement
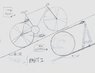
What will the scale read in these 2 examples?
The incline is 12 degrees. The bicycle weight is 14kg. The cylinder weight is 14kg.
Homework Equations
Force of 2nd pulley 'arm' is 1/2 weight
Force on incline is force X sin(angle)
The Attempt at a Solution
A scale is attached with wires to the circumference of the bicycle wheel and the bicycle frame. The line of the wire is at a tangent to the wheel. The measurement on the scale is: (14kg) (sin12) = 2.9kg
Another scale is attached similarly to the circumference of the cylinder, except the scale is attached to a frame mounted to the ground. The measurement of the scale is: .5 (14kg) (sin12) = 1.45kg