- #1
DivGradCurl
- 372
- 0
"Bifurcation Points. In many physical problems some observable quantity, such as a velocity, waveform, or chemical reaction, depends on a parameter describing the physical state. As this parameter is increased, a critical value is reached at which the velocity, or waveform, or reaction suddenly changes its character. For example, as the amount of one of the chemicals in a certain mixture is increased, spiral wave patterns of varying color suddenly emerge in an originally quiescent fluid. In many such cases the mathematical analysis ultimately leads to an equation of the form
[tex]\frac{dx}{dt} = \left( R - R_c \right) x - ax^3 \mbox{.}[/tex]
Here [tex]a[/tex] and [tex]R_c[/tex] are positive constants, and [tex]R[/tex] is a parameter that may take on various values. For example, [tex]R[/tex] may measure the amount of a certain chemical and [tex]x[/tex] may measure a chemical reaction.
(a) If [tex]R < R_c \mbox{,}[/tex] show that there is only one equilibrium solution [tex]x = 0[/tex] and that it is asymptotically stable.
(b) If [tex]R > R_c \mbox{,}[/tex] show that there are three equilibrium solutions, [tex]x=0[/tex] and [tex]x = \pm \sqrt{ \left( R - R_c \right) /a} \mbox{,}[/tex] and that the first solution is unstable while the other two are asymptotically stable.
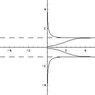
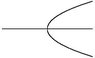
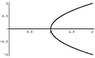
(c) Draw a graph in the [tex]Rx[/tex]-plane showing all equilibrium solutions and label each one as asymptotically stable or unstable.
The point [tex]R = R_c[/tex] is called a bifurcation point. For R < Rc one observes the asymptotically stable equilibrium solution [tex]x = 0\mbox{.}[/tex] However, this solution loses its stability as [tex]R[/tex] passes through the value Rc, and for R > Rc the asymptotically stable (and hence the observable) solutions are [tex]x = \sqrt{\left( R - R_c \right)/a}[/tex] and [tex]x = -\sqrt{\left( R - R_c \right)/a} \mbox{.}[/tex] Because of the way in which the solutions branch at [tex]R_c[/tex], this type of bifurcation is called a pitchfork bifurcation; your sketch should suggest that this name is appropriate."
My work
We are given the following:
[tex]\frac{dx}{dt} = \left( R - R_c \right) x - ax^3 \mbox{,} \qquad R_c > 0 \mbox{,} \qquad a > 0 \mbox{.}[/tex]
(a)
If [tex]R<R_c\mbox{,}[/tex] then we obtain:
[tex]f\left( x \right) = \left( R - R_c \right) x - ax^3 = 0 \Rightarrow x = 0 = \phi \left( t \right) \mbox{.}[/tex]
Note that [tex]R - R_c \neq ax^2[/tex]. Thus, [tex]\phi \left( t \right)[/tex] is the only critical point. Also, consider the following:
[tex]f ^{\prime} \left( x \right) = R - R_c - 3ax^2 \Rightarrow f ^{\prime} \left( \phi \right) = R - R_c < 0[/tex]
which implies that [tex]\phi \left( t \right)[/tex] is asymptotically stable.
(b)
If [tex]R>R_c\mbox{,}[/tex] then we obtain:
[tex] f\left( x \right) = \left( R - R_c \right) x - ax^3 = 0 \Rightarrow \left\{ \begin{array}{l} \displaystyle x = 0 = \zeta _1 (t) \mbox{,} \vspace*{6pt} \\ \displaystyle x = \sqrt{\frac{R - R_c}{a}} = \zeta _2 (t) \mbox{,} \vspace*{6pt} \\ \displaystyle x = -\sqrt{\frac{R - R_c}{a}} = \zeta _3 (t) \mbox{.} \end{array} \right.[/tex]
Also, consider the following:
[tex]f ^{\prime} \left( x \right) = R - R_c - 3ax^2 \Rightarrow \left\{ \begin{array}{l} f ^{\prime} \left( \zeta _1 \right) = R - R_c > 0 \mbox{,} \\ f ^{\prime} \left( \zeta _2 \right) = -2\left( R - R_c \right) < 0 \mbox{,} \\ f ^{\prime} \left( \zeta _3 \right) = 4\left( R - R_c \right) > 0 \mbox{,} \end{array} \right.[/tex]
which implies that [tex]\zeta _1 \left( t \right)[/tex] is an unstable critical point, and [tex]\zeta _2 \left( t \right)[/tex] is an asymptotically stable critical point, and [tex]\zeta _3 \left( t \right)[/tex] is an asymptotically stable critical point.
(c)
First, let's find any inflection points there may be.
[tex]f ^{\prime} \left( x \right) = R - R_c - 3ax^2 = 0 \Rightarrow x = \pm \sqrt{\frac{R-R_c}{3a}}[/tex]
I know how a pitchfork looks like, but I'm not sure how those inflection points are going to affect this particular picture. It'd be easier if I knew how to plot this using mathematica. Any tips?
Any help is highly appreciated.
[tex]\frac{dx}{dt} = \left( R - R_c \right) x - ax^3 \mbox{.}[/tex]
Here [tex]a[/tex] and [tex]R_c[/tex] are positive constants, and [tex]R[/tex] is a parameter that may take on various values. For example, [tex]R[/tex] may measure the amount of a certain chemical and [tex]x[/tex] may measure a chemical reaction.
(a) If [tex]R < R_c \mbox{,}[/tex] show that there is only one equilibrium solution [tex]x = 0[/tex] and that it is asymptotically stable.
(b) If [tex]R > R_c \mbox{,}[/tex] show that there are three equilibrium solutions, [tex]x=0[/tex] and [tex]x = \pm \sqrt{ \left( R - R_c \right) /a} \mbox{,}[/tex] and that the first solution is unstable while the other two are asymptotically stable.
(c) Draw a graph in the [tex]Rx[/tex]-plane showing all equilibrium solutions and label each one as asymptotically stable or unstable.
The point [tex]R = R_c[/tex] is called a bifurcation point. For R < Rc one observes the asymptotically stable equilibrium solution [tex]x = 0\mbox{.}[/tex] However, this solution loses its stability as [tex]R[/tex] passes through the value Rc, and for R > Rc the asymptotically stable (and hence the observable) solutions are [tex]x = \sqrt{\left( R - R_c \right)/a}[/tex] and [tex]x = -\sqrt{\left( R - R_c \right)/a} \mbox{.}[/tex] Because of the way in which the solutions branch at [tex]R_c[/tex], this type of bifurcation is called a pitchfork bifurcation; your sketch should suggest that this name is appropriate."
My work
We are given the following:
[tex]\frac{dx}{dt} = \left( R - R_c \right) x - ax^3 \mbox{,} \qquad R_c > 0 \mbox{,} \qquad a > 0 \mbox{.}[/tex]
(a)
If [tex]R<R_c\mbox{,}[/tex] then we obtain:
[tex]f\left( x \right) = \left( R - R_c \right) x - ax^3 = 0 \Rightarrow x = 0 = \phi \left( t \right) \mbox{.}[/tex]
Note that [tex]R - R_c \neq ax^2[/tex]. Thus, [tex]\phi \left( t \right)[/tex] is the only critical point. Also, consider the following:
[tex]f ^{\prime} \left( x \right) = R - R_c - 3ax^2 \Rightarrow f ^{\prime} \left( \phi \right) = R - R_c < 0[/tex]
which implies that [tex]\phi \left( t \right)[/tex] is asymptotically stable.
(b)
If [tex]R>R_c\mbox{,}[/tex] then we obtain:
[tex] f\left( x \right) = \left( R - R_c \right) x - ax^3 = 0 \Rightarrow \left\{ \begin{array}{l} \displaystyle x = 0 = \zeta _1 (t) \mbox{,} \vspace*{6pt} \\ \displaystyle x = \sqrt{\frac{R - R_c}{a}} = \zeta _2 (t) \mbox{,} \vspace*{6pt} \\ \displaystyle x = -\sqrt{\frac{R - R_c}{a}} = \zeta _3 (t) \mbox{.} \end{array} \right.[/tex]
Also, consider the following:
[tex]f ^{\prime} \left( x \right) = R - R_c - 3ax^2 \Rightarrow \left\{ \begin{array}{l} f ^{\prime} \left( \zeta _1 \right) = R - R_c > 0 \mbox{,} \\ f ^{\prime} \left( \zeta _2 \right) = -2\left( R - R_c \right) < 0 \mbox{,} \\ f ^{\prime} \left( \zeta _3 \right) = 4\left( R - R_c \right) > 0 \mbox{,} \end{array} \right.[/tex]
which implies that [tex]\zeta _1 \left( t \right)[/tex] is an unstable critical point, and [tex]\zeta _2 \left( t \right)[/tex] is an asymptotically stable critical point, and [tex]\zeta _3 \left( t \right)[/tex] is an asymptotically stable critical point.
(c)
First, let's find any inflection points there may be.
[tex]f ^{\prime} \left( x \right) = R - R_c - 3ax^2 = 0 \Rightarrow x = \pm \sqrt{\frac{R-R_c}{3a}}[/tex]
I know how a pitchfork looks like, but I'm not sure how those inflection points are going to affect this particular picture. It'd be easier if I knew how to plot this using mathematica. Any tips?
Any help is highly appreciated.
Last edited: