- #1
pinkfishegg
- 57
- 3
Homework Statement
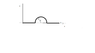
Use the Biot-Savart Law to find the magnetic field strength at the center of the semicircle in fig 35.53
Homework Equations
Bcurrent=(μ/4π)*(IΔsXr^)/r2
Bwire=μI/2πd
The Attempt at a Solution
The solution from the back of the book is
B=μI/4πd
It looks like they just added the two wires together and the the B-field of the loop in the middle is zero. I don't understand what the cross product would give you zero though. The example that derived the B-field of a wire put a point on the y-axis and used that to find R and determine the cross-product. Why would that lead to a cross product of zero for the arc?